题目内容
若不等式组
表示的平面区域是一个三角形,则a的取值范围是( )
|
分析:要确定不等式组
表示的平面区域是否一个三角形,可以先画出
,再对a值进行分类讨论,找出满足条件的实数a的取值范围.
|
|
解答: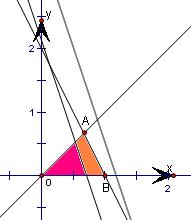 解:由题意可知:画可行域如图:
解:由题意可知:画可行域如图:
不等式组
表示的平面区域是一个三角形及其内部,
且当直线3x+y=a过直线x-y=0与直线y=0的交点O时,a=0.
表示的平面区域是一个三角形,
当直线3x+y=a过直线x-y=0与直线2x+y=2的交点A时,a=
.
表示的平面区域是一个三角形,
所以a的取值范围是:0<a≤
,
当直线3x+y=a过直线y=0与直线2x+y=2的交点B(1,0)时,a=3
表示的平面区域是一个三角形,
综上a的范围是0<a≤
或a≥3.
故选A.
 解:由题意可知:画可行域如图:
解:由题意可知:画可行域如图:不等式组
|
且当直线3x+y=a过直线x-y=0与直线y=0的交点O时,a=0.
表示的平面区域是一个三角形,
当直线3x+y=a过直线x-y=0与直线2x+y=2的交点A时,a=
| 8 |
| 3 |
表示的平面区域是一个三角形,
所以a的取值范围是:0<a≤
| 8 |
| 3 |
当直线3x+y=a过直线y=0与直线2x+y=2的交点B(1,0)时,a=3
表示的平面区域是一个三角形,
综上a的范围是0<a≤
| 8 |
| 3 |
故选A.
点评:平面区域的形状问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合分类讨论的思想,针对图象分析满足条件的参数的取值范围.

练习册系列答案
相关题目