Question

若不等式组

x-y≥0 2x+y≤2 x+y≤m y≥0

，表示的平面区域是一个三角形，则实数m的取值范围是（　　）

• A．m≥

  4

  3

• B．0＜m≤1
• C．1≤m≤

  4

  3

• D．0＜m≤1或m≥

  4

  3

Answer 1

分析：作出不等式组对应的平面区域，利用平面区域为三角形，建立条件关系即可求m的取值范围．

解答：解：先作出不等式组

x-y≥0 2x+y≤2 y≥0

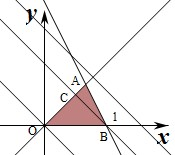
对应的平面区域如图：（阴影部分OAB），
∵不等x+y≤m表示的平面区域为直线x+y=m，的左下面．
∴要使不等式组表示的平面区域是一个三角形，
则直线x+y=m必须在线段OC之间移动或在点A的右上方．
由图象可知B（1，0），此时m=1+0=1，
由

x-y=0 2x+y=2

，解得

x= 2 3 y= 2 3

，即A（

2

3

，

2

3

），
此时m=

2

3

+

2

3

=

4

3

，
∴满足条件的m范围是0＜m≤1或m≥

4

3

．
故选：D．

点评：本题主要考查线性规划的应用，利用二元一次不等式组和平面区域之间的关系是解决本题的关键，注意利用数形结合．