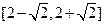题目内容
若关于x的方程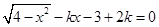 有且只有两个不同的实数根,则实数k的取值范围是
有且只有两个不同的实数根,则实数k的取值范围是
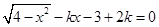 有且只有两个不同的实数根,则实数k的取值范围是
有且只有两个不同的实数根,则实数k的取值范围是A. | B. | C. | D. |
D
先将方程根的情况转化为一个半圆与一条直线交点的情况,再用数形结合,先求出相切时的斜率,再得到有两个交点的情况.
解:
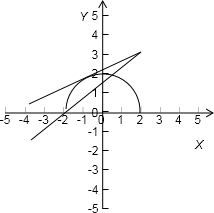
将方程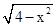 -kx-3+2k=0转化为:
-kx-3+2k=0转化为:
半圆y=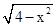 ,与直线y=kx+3-2k有两个不同交点.
,与直线y=kx+3-2k有两个不同交点.
当直线与半圆相切时,有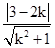 =2
=2
k=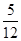
∴半圆y=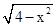 与直线y=kx+3-2k有两个不同交点时.
与直线y=kx+3-2k有两个不同交点时.
直线y=kx+3-2k=k(x-2)+3,一定过(2,3),由图象知直线过(-2,0)时直线的斜率k取最大值为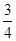 k∈(
k∈(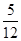 ,
,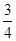 ]
]
故选D
解:

将方程
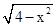 -kx-3+2k=0转化为:
-kx-3+2k=0转化为:半圆y=
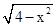 ,与直线y=kx+3-2k有两个不同交点.
,与直线y=kx+3-2k有两个不同交点.当直线与半圆相切时,有
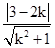 =2
=2k=
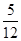
∴半圆y=
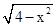 与直线y=kx+3-2k有两个不同交点时.
与直线y=kx+3-2k有两个不同交点时.直线y=kx+3-2k=k(x-2)+3,一定过(2,3),由图象知直线过(-2,0)时直线的斜率k取最大值为
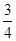 k∈(
k∈(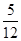 ,
,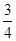 ]
]故选D

练习册系列答案
相关题目
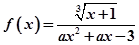 的定义域是R,则实数a的取值范围是( )
的定义域是R,则实数a的取值范围是( )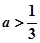
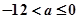
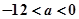
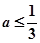
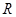 上的偶函数
上的偶函数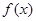 ,对于任意的
,对于任意的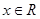 都满足:
都满足: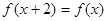 ,当
,当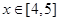 时
时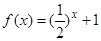 ,则( )
,则( )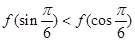
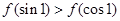
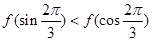
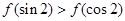
 的一个正数零点附近的函数值用二分法计算,其参
的一个正数零点附近的函数值用二分法计算,其参
 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为 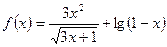 的定义域为____________。
的定义域为____________。 ,函数
,函数 有最小值,则不等式
有最小值,则不等式
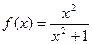 ,
, .
. 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟
,可以用随机模拟 ,先产生两组(每组
,先产生两组(每组 个)区间
个)区间 和
和 ,由此得到
,由此得到 。再数出其中满足
。再数出其中满足 的点数
的点数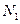 ,那么由随机模拟方法计算积分
,那么由随机模拟方法计算积分 若有
若有 则
则 的取值范围为( )
的取值范围为( )