题目内容
(本小题满分12分)
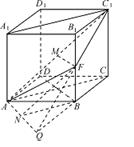
如右图所示,已知直四棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() ,
,![]() ,F为
,F为![]() 的中点,M为线段
的中点,M为线段![]() 的中点。
的中点。
(1)求证:直线MF![]() 平面ABCD
平面ABCD
(2)求证:直线MF![]() 平面
平面![]()
(3)求平面![]() 与平面ABCD所成二面角的大小
与平面ABCD所成二面角的大小

(1)略(2)略(3) ![]() 或
或![]()
解析:
解法一:(1)设AC与BD交于点O,因为点M、F分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,
,![]() ――――――――3分
――――――――3分
(2)因为底面为菱形且![]() ,所以四边形
,所以四边形![]() 与
与![]() 全等,
全等,
又点F为![]() 中点,所以
中点,所以![]() ,在等腰△
,在等腰△![]() 中,
中,![]()
因为![]() ,所以
,所以![]() ,可得
,可得![]() ,
,
所以![]() (线面垂直判定定理)
(线面垂直判定定理)
――――――――――――――――――――7分
(3)延长![]() ,连接AQ,则AQ为平面
,连接AQ,则AQ为平面![]() 与平面ABCD的交线.
与平面ABCD的交线.
所以FB为△![]() 的中位线, 则QB=BC,设底面菱形边长为a,可得AB=QB=a,
的中位线, 则QB=BC,设底面菱形边长为a,可得AB=QB=a,
又![]() 所以
所以![]() 那么△ABQ为等边三角形.
那么△ABQ为等边三角形.
取AQ中点N,连接BN、FN,则![]() 为所求二面角的平面角或其补角.
为所求二面角的平面角或其补角.
在△FNB中, 
![]() ――――――11分
――――――11分
即所求平面![]() 与平面ABCD所成二面角的平面角为
与平面ABCD所成二面角的平面角为![]() 或
或![]() ―――――――12分
―――――――12分
(说明:答对一个即给满分)
解法二:设![]() ,因为M、O分别为
,因为M、O分别为![]() 的中点,∴MO∥
的中点,∴MO∥![]()
又由直四棱柱知![]() ,∴
,∴![]()
在棱形ABCD中,![]() ,∴OB、OC、OM两两垂直,故可以O为原点,OB、OC、OM所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示。―――――――――2分
,∴OB、OC、OM两两垂直,故可以O为原点,OB、OC、OM所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示。―――――――――2分
若设![]() ,则B
,则B![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)由F、M分别为![]() 中点可知
中点可知![]() ,M(0,0,1)
,M(0,0,1)
∴![]() (1,0,0)=
(1,0,0)=![]() ,又因为
,又因为![]() 和
和![]() 不共线,∴
不共线,∴![]() ∥OB
∥OB
又因为![]() ,OB
,OB![]() 平面ABCD,∴MF∥平面ABCD――――――――5分
平面ABCD,∴MF∥平面ABCD――――――――5分
(2)![]() ,而(1,0,0)为平面yOz(亦即平面
,而(1,0,0)为平面yOz(亦即平面![]() )的法向量
)的法向量
∴直线MF⊥平面![]() ――――――――――――――――――――――――8分
――――――――――――――――――――――――8分
(3)![]() 为平面ABCD的法向量,
为平面ABCD的法向量,
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则![]() ,
,
由![]() ,
,![]() ,得:
,得:![]()
令y=1,得z=![]() ,此时
,此时![]()
设平面![]() 与平面ABCD所成二面角的大小为
与平面ABCD所成二面角的大小为![]() ,
,
则
所以![]() 或
或![]() ,即平面
,即平面![]() 与平面ABCD所成二面角的大小为
与平面ABCD所成二面角的大小为![]() 或
或![]() ――12分
――12分
(说明:答对一个即给满分)

