题目内容
3.已知双曲线$\frac{{x}^{2}}{a^2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(4,0),若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则a的取值范围是0<a≤2.分析 若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率.根据这个结论可以求出b2≥3a2,利用c=4,即可求出a的取值范围.
解答 解:∵过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,
∴该直线的斜率的绝对值小于等于渐近线的斜率,
∴$\frac{b}{a}$≥$\sqrt{3}$,
∴b2≥3a2,
∵c=4
∴16≥4a2,
∴0<a≤2
故答案为:0<a≤2.
点评 本题考查双曲线的性质及其应用,解题时要注意挖掘隐含条件.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,长轴为2$\sqrt{3}$,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{3}$+y2=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 |
11.将$\root{3}{2^2}$化成分数指数幂为( )
| A. | ${2^{\frac{3}{2}}}$ | B. | $2^{-\frac{1}{2}}$ | C. | $2^{\frac{1}{3}}$ | D. | $2^{\frac{2}{3}}$ |
8.顶点在x轴上,两顶点间的距离为4,离心率e=$\frac{\sqrt{5}}{2}$的双曲线与直线y=kx(k∈R)无交点,则实数k的取值范围为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | (-∞,-$\frac{1}{2}$]∪[$\frac{1}{2}$,∞) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
15.已知a>0,a≠1,则f(x)=loga$\frac{2x+1}{x-1}$的图象恒过点( )
| A. | (1,0) | B. | (-2,0) | C. | (-1,0) | D. | (1,4) |
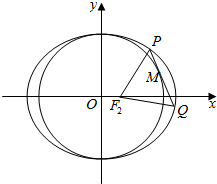 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点($\frac{3\sqrt{2}}{2}$,2)在椭圆上.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点($\frac{3\sqrt{2}}{2}$,2)在椭圆上.