题目内容
已知椭圆 ,椭圆
,椭圆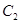 以
以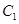 的长轴为短轴,且与
的长轴为短轴,且与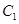 有相同的离心率.
有相同的离心率.
(1)求椭圆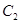 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆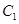 和
和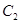 上,
上, 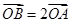 ,求直线
,求直线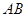 的方程.
的方程.
(1)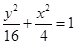 ;(2)
;(2)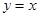 或
或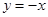
解析试题分析:(1)由题意可设,所求椭圆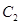 的方程为
的方程为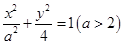 ,且其离心率可由椭圆
,且其离心率可由椭圆 的方程知
的方程知 ,因此
,因此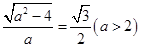 ,解之得
,解之得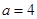 ,从而可求出椭圆
,从而可求出椭圆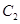 的方程为
的方程为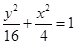 .
.
(2)由题意知,所求直线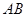 过原点,又椭圆
过原点,又椭圆 短半轴为1,椭圆
短半轴为1,椭圆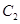 的长半轴为4,所以直线
的长半轴为4,所以直线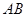 不与
不与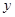 轴重合,即直线
轴重合,即直线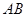 的斜率存在,可设直线
的斜率存在,可设直线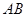 的斜率为
的斜率为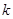 ,直线
,直线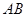 的方程为
的方程为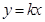 ,又设点
,又设点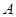 、
、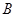 的坐标分别为
的坐标分别为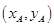 、
、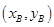 ,分别联立直线
,分别联立直线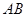 与椭圆
与椭圆 、
、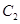 的方程消去
的方程消去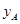 、
、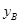 可得
可得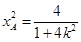 ,
,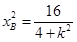 ,又
,又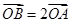 得
得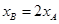 ,即
,即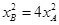 ,所以
,所以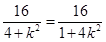 ,解得
,解得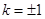 ,从而可求出直线
,从而可求出直线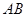 的直线方程为
的直线方程为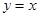 或
或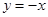 .
.
试题解析:(1)由已知可设椭圆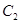 的方程为
的方程为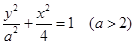
其离心率为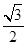 ,故
,故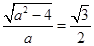 ,则
,则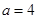
故椭圆的方程为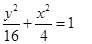 5分
5分
(2)解法一 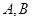 两点的坐标分别记为
两点的坐标分别记为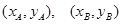
由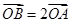 及(1)知,
及(1)知, 三点共线且点
三点共线且点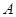 ,
,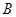 不在
不在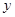 轴上,
轴上,
因此可以设直线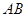 的方程为
的方程为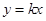
将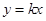 代入
代入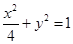 中,得
中,得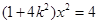 ,所以
,所以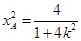
将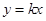 代入
代入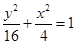 中,则
中,则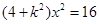 ,所以
,所以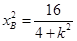
由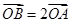 ,得
,得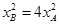 ,即
,即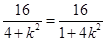
解得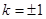 ,故直线
,故直线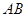 的方程为
的方程为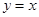 或
或 12分
12分
解法二 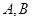 两点的坐标分别记为
两点的坐标分别记为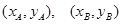
由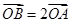 及(1)知,
及(1)知, 三点共线且点
三点共线且点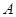 ,
,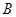 不在
不在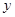 轴上,
轴上,
因此可以设直线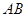

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
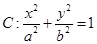
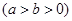 的离心率为
的离心率为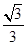 ,直线
,直线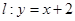 与圆
与圆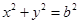 相切.
相切.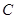 的方程;
的方程;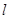 与椭圆
与椭圆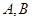 ,求弦长
,求弦长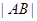 .
. 中,已知
中,已知 分别是椭圆
分别是椭圆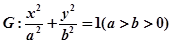 的左、右焦点,椭圆
的左、右焦点,椭圆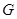 与抛物线
与抛物线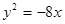 有一个公共的焦点,且过点
有一个公共的焦点,且过点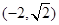 .
.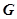 的方程;
的方程;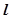 与椭圆
与椭圆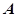 、
、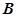 两点,若
两点,若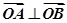 (
(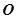 为坐标原点),试判断直线
为坐标原点),试判断直线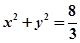 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.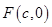 是椭圆
是椭圆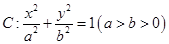 的右焦点;圆
的右焦点;圆 与
与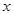 轴交于
轴交于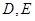 两点,其中
两点,其中 是椭圆
是椭圆 的左焦点.
的左焦点.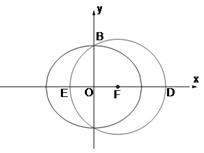
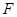 与
与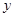 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点 关于
关于 与圆
与圆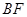 与圆
与圆 ,若
,若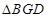 的面积为
的面积为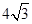 ,求椭圆
,求椭圆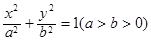 的离心率为
的离心率为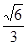 ,长轴长为
,长轴长为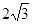 .
.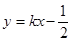 交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足
交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足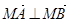 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由. 的中心在原点,焦点在
的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为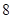 的正方形(记为
的正方形(记为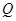 )
) 是直线
是直线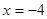 与
与 与椭圆
与椭圆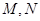 两点,当线段
两点,当线段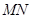 的中点落在正方形
的中点落在正方形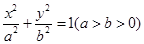 ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F(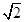 ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.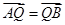 且
且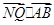 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.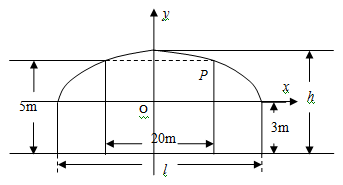
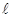 是多少?
是多少?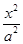 +
+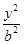 =1的面积公式为S=
=1的面积公式为S=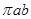 ,柱体体积为底面积乘以高。)
,柱体体积为底面积乘以高。)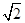 倍,试确定M、N的位置以及
倍,试确定M、N的位置以及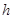 的值,使总造价最少。
的值,使总造价最少。 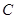 的中心在原点
的中心在原点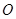 ,离心率
,离心率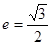 ,右焦点为
,右焦点为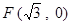 .
.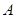 ,在椭圆
,在椭圆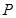 ,使得向量
,使得向量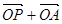 与
与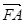 共线?若存在,求直线
共线?若存在,求直线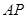 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.