题目内容

设函数g（x）=x²-2（x∈R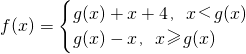）， $数学公式$ 则f（x）的值域是________．

$\text{[math]}$
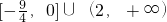
分析：当x＜g（x）时，x＞2 或x＜-1，f（x）=g（x）+x+4=x²-2+x+4=x²+x+2=（x+0.5）²+1.75，其值域为：（2，+∞）．当x≥g（x）时，-1≤x≤2，f（x）=g（x）-x=x²-2-x=（x-0.5）²-2.25，其值域为：[-2.25，0]．由此能得到函数值域．
解答：当x＜g（x），即x＜x²-2，（x-2）（x+1）＞0时，x＞2 或x＜-1，
f（x）=g（x）+x+4=x²-2+x+4=x²+x+2=（x+0.5）²+1.75，
∴其最小值为f（-1）=2
其最大值为+∞，
因此这个区间的值域为：（2，+∞）．
当x≥g（x）时，-1≤x≤2，
f（x）=g（x）-x=x²-2-x=（x-0.5）²-2.25
其最小值为f（0.5）=-2.25
其最大值为f（2）=0
因此这区间的值域为：[-2.25，0]．
综合得：函数值域为：[-2.25，0]U（2，+∞）
点评：本题考查f（x）的值域的求法．解题时要认真审题，注意分类讨论思想的合理运用．

练习册系列答案

锦绣文章系列答案

精讲精练阅读理解与完形填空系列答案

阅读理解与完型填空加油站系列答案

开卷8分钟英语阅读理解与完形填空系列答案

开路先锋系列答案

课内外文言文阅读系列答案

名师点睛课堂全解系列答案

课外阅读试题精选系列答案

快捷语文系列答案

乐多英语专项突破系列答案

相关题目

已知函数f（x）=

（a∈R且x≠a）．
（Ⅰ）求证：f（x）+f（2a-x）=-2对定义域内的所有x都成立；
（Ⅱ）当f（x）的定义域为[a+

，a+1]时，求证：f（x）的值域为[-3，-2]；
（Ⅲ）设函数g（x）=x²+|（x-a）•f（x）|，当a=-1时，求g（x）的最小值．

已知函数f(x)=

(m，n∈R)在x=1处取得极值2．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若函数f（x）在区间（t，2t+1）上是单调函数，求实数t的取值范围；
（Ⅲ）设函数g（x）=x²-2ax+a，若对于任意的x₁∈R，总存在x₂∈[-1，1]，使得g（x₂）≤f（x₁），求实数a的取值范围．

已知函数f（x）是定义在R上的偶函数，且x≥0时，f（x）=(

)x．
（Ⅰ）求函数f（x）的值域A；
（Ⅱ）设函数g（x）=

的定义域为集合B，若A⊆B，求实数a的取值范围．

（2008•奉贤区一模）我们将具有下列性质的所有函数组成集合M：函数y=f（x）（x∈D），对任意x，y，

∈D均满足f(

[f(x)+f(y)]，当且仅当x=y时等号成立．
（1）若定义在（0，+∞）上的函数f（x）∈M，试比较f（3）+f（5）与2f（4）大小．
（2）设函数g（x）=-x²，求证：g（x）∈M．
（3）已知函数f（x）=log₂x∈M．试利用此结论解决下列问题：若实数m、n满足2^m+2ⁿ=1，求m+n的最大值．

已知函数：f(x)=

(a∈R且x≠a)．
（1）证明：f（x）+2+f（2a-x）=0对定义域内的所有x都成立；
（2）当f（x）的定义域为[a+

，a+1]时，求证：f（x）的值域为[-3，-2]；
（3）（理）设函数g（x）=x²+|（x-a）f（x）|，求g（x）的最小值．
（4）（文）设函数g（x）=x²+（x-a）f（x），其中x≤a-1，求g（x）的最小值．