题目内容
(1)椭圆C:(2)由(1)类比可得如下真命题:双曲线C:![]() -
-![]() =1(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:AN·BM为定值.请写出这个定值(不要求给出解题过程).
=1(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:AN·BM为定值.请写出这个定值(不要求给出解题过程).
(1)证明:设点P(x0,y0),x0≠±a.依题意,得A(-a,0),B(a,0),
∴直线PA的方程为y=![]() (x+a).
(x+a).
令x=0,得ym=![]() ,4分同理得yn=
,4分同理得yn=![]() ,
,
∴ymyn=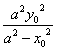 .∵点P(x0,y0)是椭圆C上一点,∴
.∵点P(x0,y0)是椭圆C上一点,∴![]() =1.∴y02=
=1.∴y02=![]() (a2-x02).
(a2-x02).
∴ymyn=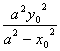 =b2.8分∵
=b2.8分∵![]() =(a,yn),
=(a,yn),![]() =(-a,ym),∴
=(-a,ym),∴![]() ·
·![]() =-a2+ymyn=b2-a2.10分
=-a2+ymyn=b2-a2.10分
(2)-(a2+b2).

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
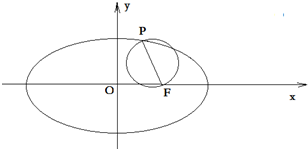 (2011•通州区一模)已知椭圆C:
(2011•通州区一模)已知椭圆C: