��Ŀ����
19����֪����C��x2+y2=1��������C�ϵĵ㰴����任$\left\{\begin{array}{l}{x��=2x}\\{y��=3y}\end{array}\right.$�õ�����C�䣻��ֱ������ϵԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ֱ��l�ļ�����ϵ�����Ǧѣ�2cos��+sin�ȣ�=10����1��д������C���ֱ��l����ͨ���̣�
��2��������C���ϵĵ�M��ֱ��l��������ֵ����ʱ��M�����꣮
���� ��1������C��x2+y2=1��������C�ϵĵ㰴����任$\left\{\begin{array}{l}{x��=2x}\\{y��=3y}\end{array}\right.$�ɵ�$\left\{\begin{array}{l}{x=\frac{1}{2}{x}^{��}}\\{y=\frac{1}{3}{y}^{��}}\end{array}\right.$����������C�ķ��̿ɵõ�����C�䣻ֱ��l�ļ�����ϵ�����Ǧѣ�2cos��+sin�ȣ�=10����$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$���뼴�ɵõ�ֱ�����귽�̣�
��2������ֱ��2x+y-10=0ƽ��������ԲC���е�ֱ�߷���Ϊ��2x+y-t=0����y=t-2x��������C�ķ��̿ɵã�25x2-16tx+4t2-36=0�����=0�����t���ɵ��е�M�����ɵó���M��ֱ��l��������ֵ��
��� �⣺��1������C��x2+y2=1��������C�ϵĵ㰴����任$\left\{\begin{array}{l}{x��=2x}\\{y��=3y}\end{array}\right.$�ɵ�$\left\{\begin{array}{l}{x=\frac{1}{2}{x}^{��}}\\{y=\frac{1}{3}{y}^{��}}\end{array}\right.$����������C�ķ��̿ɵã�$\frac{��{x}^{��}��^{2}}{4}+\frac{��{y}^{��}��^{2}}{9}=1$���õ�����C�䣻
ֱ��l�ļ�����ϵ�����Ǧѣ�2cos��+sin�ȣ�=10����Ϊ2x+y-10=0��
��2������ֱ��2x+y-10=0ƽ��������ԲC���е�ֱ�߷���Ϊ��2x+y-t=0��
��y=t-2x��������C�ķ��̿ɵã�25x2-16tx+4t2-36=0����*��
���=0�����t=��5��ȡt=-5��
�̣�*����Ϊ����5x+8��2=0��
���x=-$\frac{8}{5}$��y=$-\frac{9}{5}$��
���е�M$��-\frac{8}{5}��-\frac{9}{5}��$��
���M��ֱ��l��������ֵ=$\frac{|-\frac{16}{5}-\frac{9}{5}-10|}{\sqrt{5}}$=3$\sqrt{5}$��
���� ���⿼���˰Ѽ����귽�̻�Ϊֱ�Ƿ��̡�ֱ������Բ�����á��㵽ֱ�ߵľ��빫ʽ���ƽ�е�ֱ�ߵ�б��֮��Ĺ�ϵ��������������������������������е��⣮

| A�� | ��0��$\frac{\sqrt{5}}{5}$�� | B�� | ��$\frac{\sqrt{5}}{5}$��1�� | C�� | ��$\frac{\sqrt{7}}{7}$��1�� | D�� | ��0��$\frac{\sqrt{7}}{7}$�� |
| A�� | $\sqrt{37}$ | B�� | $\sqrt{13}$ | C�� | 3$\sqrt{7}$ | D�� | 2$\sqrt{6}$ |
 ��ͼ������ADMN�����ABCD����ƽ�滥�ഹֱ����E���߶�AB�ϣ�AB=2AD=6��
��ͼ������ADMN�����ABCD����ƽ�滥�ഹֱ����E���߶�AB�ϣ�AB=2AD=6��
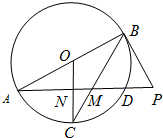 ��ͼAB��ԲO��ֱ������B��ԲO�����߽���AD���ӳ����ڵ�P��MΪAD��һ�㣬��PB=PM=6��PD=4������BM���ӳ���ԲO�ڵ�C������OC��AD�ڵ�N����CN=$\frac{{\sqrt{5}}}{2}$��
��ͼAB��ԲO��ֱ������B��ԲO�����߽���AD���ӳ����ڵ�P��MΪAD��һ�㣬��PB=PM=6��PD=4������BM���ӳ���ԲO�ڵ�C������OC��AD�ڵ�N����CN=$\frac{{\sqrt{5}}}{2}$��