题目内容
已知函数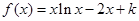 在
在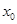 处取得极值,且
处取得极值,且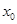 恰好是
恰好是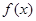 的一个零点.
的一个零点.
(Ⅰ)求实数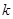 的值,并写出函数
的值,并写出函数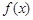 的单调区间;
的单调区间;
(Ⅱ)设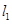 、
、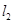 分别是曲线
分别是曲线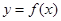 在点
在点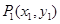 和
和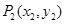 (其中
(其中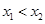 )处的切线,且
)处的切线,且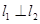 .
.
①若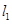 与
与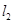 的倾斜角互补,求
的倾斜角互补,求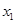 与
与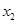 的值;
的值;
②若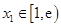 (其中
(其中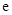 是自然对数的底数),求
是自然对数的底数),求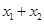 的取值范围.
的取值范围.
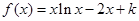 在
在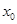 处取得极值,且
处取得极值,且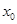 恰好是
恰好是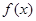 的一个零点.
的一个零点.(Ⅰ)求实数
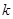 的值,并写出函数
的值,并写出函数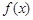 的单调区间;
的单调区间;(Ⅱ)设
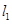 、
、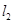 分别是曲线
分别是曲线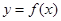 在点
在点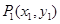 和
和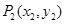 (其中
(其中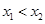 )处的切线,且
)处的切线,且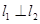 .
.①若
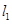 与
与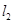 的倾斜角互补,求
的倾斜角互补,求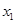 与
与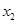 的值;
的值;②若
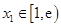 (其中
(其中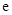 是自然对数的底数),求
是自然对数的底数),求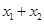 的取值范围.
的取值范围.(Ⅰ)增区间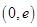 ,减区间
,减区间 ;(Ⅱ)①
;(Ⅱ)①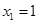 ,
, ;②
;②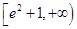 .
.
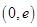 ,减区间
,减区间 ;(Ⅱ)①
;(Ⅱ)①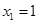 ,
, ;②
;②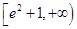 .
.试题分析:(Ⅰ)根据函数
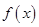 在
在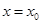 处取得极值有
处取得极值有 ,以及
,以及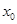 是函数
是函数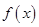 的一个零点,有
的一个零点,有 ,由这两个等式列方程组求
,由这两个等式列方程组求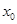 和
和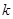 ,从而确定函数
,从而确定函数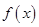 ,进而利用导数求函数
,进而利用导数求函数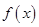 的单调增区间与减区间;(Ⅱ)①在(Ⅰ)函数
的单调增区间与减区间;(Ⅱ)①在(Ⅰ)函数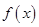 的解析式确定的基础上,由
的解析式确定的基础上,由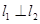 得
得 ,由
,由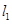 与
与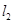 的倾斜角互补得到
的倾斜角互补得到 以及
以及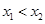 可以求出
可以求出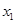 与
与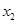 的值;②根据
的值;②根据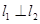 这个条件确定
这个条件确定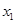 与
与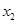 的关系,再进行适当转化利用基本不等式或函数的最值的思想求
的关系,再进行适当转化利用基本不等式或函数的最值的思想求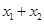 的取值范围.
的取值范围.试题解析:(Ⅰ)
 ,
,由已知得:
 得
得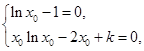 3分
3分解得
 . 4分
. 4分当
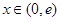 时,
时,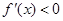 ,当
,当 时,
时, ,
,所以函数
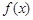 单调减区间是
单调减区间是 ,增区间是
,增区间是 . 6分
. 6分(Ⅱ)由(Ⅰ)得
 ,
, 依题意,直线
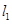 和
和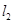 的斜率分别为
的斜率分别为 和
和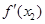 ,
,因为
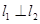 ,所以
,所以 ,
,所以
 .(*)
.(*)①因为
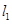 与
与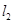 的倾斜角互补,所以
的倾斜角互补,所以 ,
, 即
 ,(**) 8分
,(**) 8分由(*)(**),结合
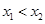 ,解得
,解得 ,
, ,
,即
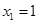 ,
, . 10分
. 10分②因为
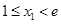 ,所以
,所以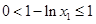 ,
, ,
,所以
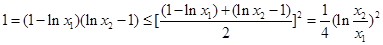 ,
,所以
 ,当且仅当
,当且仅当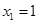 时,等号成立.
时,等号成立.又因为
 ,当且仅当
,当且仅当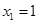 时,等号成立.
时,等号成立.所以
 . 14分
. 14分
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C. 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程; 的面积的最大值。
的面积的最大值。 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度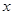 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度 时,求函数
时,求函数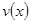 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时). 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为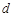 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为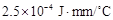 .)
.) ,
,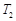 ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
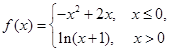 ,若
,若 ,则
,则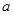 的取值范围是( )
的取值范围是( )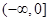
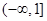
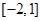
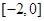
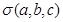 满足
满足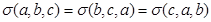 ,则称
,则称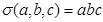 ; ②
; ②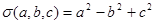 ;
;
 是
是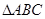 的内角).
的内角).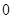
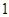
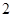
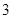
 的所有零点之和等于( )
的所有零点之和等于( )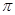
 .
. 时,
时,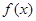 取得极值,求
取得极值,求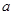 的值;
的值; ,当
,当 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明 (
( ).
).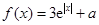 (
(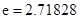 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为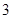 .
.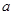 的值;
的值;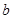
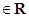 且
且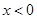 ,试解关于
,试解关于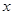 的不等式
的不等式 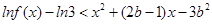 ;
;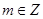 且
且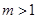 .若存在实数
.若存在实数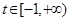 ,使得对任意的
,使得对任意的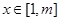 ,都有
,都有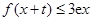 ,试求
,试求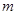 的最大值.
的最大值.