题目内容
三角形有一个角是60°，夹这个角的两边的长度分别为8和5，则此三角形内切圆的面积为
- A.3π
- B.6π
- C.12π
- D.
π
A
分析：分析题设条件可以先求出第三边的长，再由三角形的内切圆的几何性质利用等面积法求出内切轴圆的半径．
解答：由已知第三边的长度为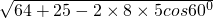
=7，
故有
×8×5×sin600=×r（5+7+8）
∴r=，
故三角形内切圆的面积为3π．
故选A．
点评：本题用等面积法建立了关于三角形内切圆半径的方程求出其半径，这是在这个背景下求内切圆半径的最优方式．
分析：分析题设条件可以先求出第三边的长，再由三角形的内切圆的几何性质利用等面积法求出内切轴圆的半径．
解答：由已知第三边的长度为
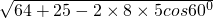=7，故有
×8×5×sin600=×r（5+7+8）∴r=
，故三角形内切圆的面积为3π．
故选A．
点评：本题用等面积法建立了关于三角形内切圆半径的方程求出其半径，这是在这个背景下求内切圆半径的最优方式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
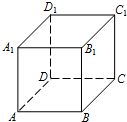在直四棱柱ABCD-A1B1C1D1中，底面是有一个角为60°的菱形，AA1=AB，从顶点中取出三个能构成不同直角三角形的个数有（ ）个．三角形有一个角是60°，夹这个角的两边的长度分别为8和5，则此三角形内切圆的面积为（ ）
| A、3π | ||
| B、6π | ||
| C、12π | ||
D、
|
，或{0}
③对于命题p且q，若p假q真，则p且q为假 ④“有两条边相等且有一个角是60°”是“一个三角形为等边三角形”的充要条件