题目内容
【题目】要使g(x)=3x+1+t的图象不经过第二象限,则t的取值范围为( )
A.t≤﹣1
B.t<﹣1
C.t≤﹣3
D.t≥﹣3
【答案】C
【解析】解:指数函数y=3x过定点(0,1),
函数g(x)=3x+1+t过定点(0,3+t)且为增函数,要使g(x)=3x+1+t的图象不经过第二象限,
只须函数g(x)=3x+1+t与y轴的交点的纵坐标小于等于0即可,
如图所示,
即图象不过第二象限,则3+t≤0
∴t≤﹣3,
则t的取值范围为:t≤﹣3.
故选C.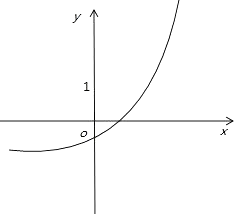
【考点精析】本题主要考查了指数函数的图像与性质的相关知识点,需要掌握a0=1, 即x=0时,y=1,图象都经过(0,1)点;ax=a,即x=1时,y等于底数a;在0<a<1时:x<0时,ax>1,x>0时,0<ax<1;在a>1时:x<0时,0<ax<1,x>0时,ax>1才能正确解答此题.

练习册系列答案
相关题目

