题目内容
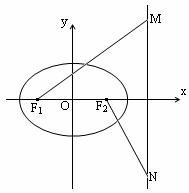
如图,椭圆C : 的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6
的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6
(1)求椭圆C的方程;
(2)设直线AF1与椭圆交于另一点B,与y轴交于一点C,记 ,若点A在第一象限,求m+n的取值范围;
,若点A在第一象限,求m+n的取值范围;
 的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6
的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6(1)求椭圆C的方程;
(2)设直线AF1与椭圆交于另一点B,与y轴交于一点C,记
 ,若点A在第一象限,求m+n的取值范围;
,若点A在第一象限,求m+n的取值范围;
解:(1)∵F1,F2是A1A2的三等分点
∴a=3c
又∵|AF1|+|AF2|=6
∴a=3
∴b2=8
∴椭圆C的方程为: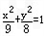
(2)F1(-1,0),当直线与x轴重合时,显然不合题意,
当直线不与x轴重合时,设直线AF1:x=my-1
代入到椭圆方程并消元整理得:(8m2+9)y2-16my-64=0 …………①
△=162×9(m2+1)>0恒成立;
设A(x1,y1),B(x2,y2),则y1,y2是方程①的两个解,
由韦达定理得: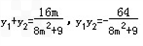
在x=my-1中令x=0得C点坐标为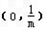
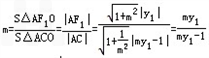 (∵A在第一象限∴x1=my1-1>0,y1>0)
(∵A在第一象限∴x1=my1-1>0,y1>0)
同理: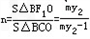
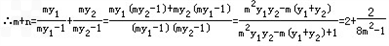
∵A在第一象限
∴C点在椭圆内部
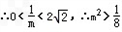
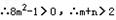
∴m+n的取值范围是(2,+∞)
∴a=3c
又∵|AF1|+|AF2|=6
∴a=3
∴b2=8
∴椭圆C的方程为:
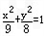
(2)F1(-1,0),当直线与x轴重合时,显然不合题意,
当直线不与x轴重合时,设直线AF1:x=my-1
代入到椭圆方程并消元整理得:(8m2+9)y2-16my-64=0 …………①
△=162×9(m2+1)>0恒成立;
设A(x1,y1),B(x2,y2),则y1,y2是方程①的两个解,
由韦达定理得:
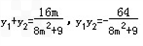
在x=my-1中令x=0得C点坐标为
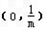
 (∵A在第一象限∴x1=my1-1>0,y1>0)
(∵A在第一象限∴x1=my1-1>0,y1>0)同理:
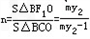
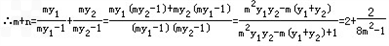
∵A在第一象限
∴C点在椭圆内部
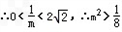
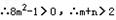
∴m+n的取值范围是(2,+∞)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
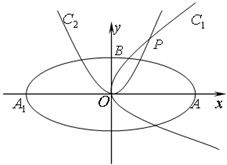 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P. ,求
,求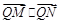 的最小值.
的最小值.