题目内容
已知椭圆
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
<e<1.
解析:
设M(x,y),则
=(x,y),
=(x-a,y).
∵⊥,
∴0=·=x(x-a)+y2.
由椭圆方程得y2=b2-
x2代入得c2x2-a3x+a2b2=0.
解得x=a或
.
由题意0<<a.
∴b2<c2.∴a2-c2<c2.
解得e2=
>
.
∴<e<1.
练习册系列答案
阅读快车系列答案
相关题目
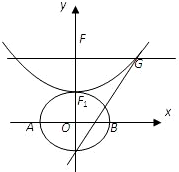设b＞0，椭圆方程为
+
=1的左焦点为F,过点F的直线交椭圆于A,B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D,E两点.
,求直线AB的斜率.
+
=1的左焦点为F,过点F的直线交椭圆于A,B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D,E两点.
,求直线AB的斜率.
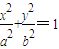（a＞b＞0），M为椭圆上的一个动点，F1、F2分别为椭圆的左、右焦点，A、B分别为椭圆的一个长轴端点与短轴的端点．当MF2⊥F1F2时，原点O到直线MF1的距离为
|OF1|．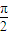
；
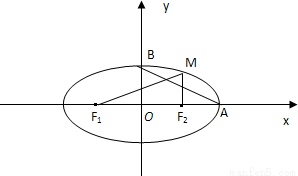
=1的离心率等于
，点P（2，
）在椭圆上。
：x=t，使得直线