题目内容
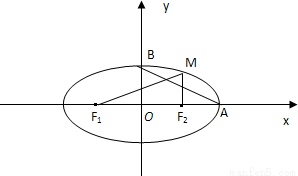
如图,已知椭圆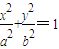 (a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为
(a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为 |OF1|.
|OF1|.(1)求a,b满足的关系式;
(2)当点M在椭圆上变化时,求证:∠F1MF2的最大值为
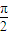 ;
;(3)设圆x2+y2=r2(0<r<b),G是圆上任意一点,过G作圆的切线交椭圆于Q1,Q2两点,当OQ1⊥OQ2时,求r的值.(用b表示)
【答案】分析:(1)设F1(-c,0),F2(c,0),A(a,c),B(0,b),因为MF2⊥F1F2,所以点M坐标为  ,由此能够求出a=
,由此能够求出a= .
.
(2)设MF1=m,MF2=n,m+n=2a,由余弦定理得 =
= .因为
.因为 ,所以cos∠F1MF2≥0,由此能够证明:∠F1MF2的最大值为
,所以cos∠F1MF2≥0,由此能够证明:∠F1MF2的最大值为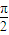 .
.
(3)设G(rcosθ,rsinθ)圆上任意一点,过G点的切线交该椭圆于Q1(x1,x2),Q2(x2,y2),则切线l的法向量为(rcosθ,rsinθ),直线l的方程为xcosθ+ysinθ-r=0,联立方程组 ,能够推导出r=
,能够推导出r= .
.
解答:解:(1)设F1(-c,0),F2(c,0),A(a,c),B(0,b),
因为MF2⊥F1F2,所以点M坐标为 ,
,
所以MF1方程b2x-2axy+b2c=0,
O到MF1距离 ,整理得2b4=a2c2,
,整理得2b4=a2c2,
所以 解得a=
解得a=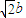 .
.
(2)设MF1=m,MF2=n,m+n=2a,
由余弦定理得
=
= .
.
因为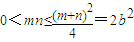 ,
,
所以cos∠F1MF2≥0,
当且仅当m=n=a=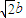 ,cos∠F1MF2=0,
,cos∠F1MF2=0,
由三角形内角及余弦单调性知有最大值 .
.
(3)设G(rcosθ,rsinθ)圆上任意一点,过G点的切线交该椭圆于Q1(x1,x2),Q2(x2,y2),
则切线l的法向量为(rcosθ,rsinθ),直线l的方程为xcosθ+ysinθ-r=0,
联立方程组 ,
,
①cosθ=0时,|OG|=|Q1G|=|Q2G|,所以r= ,即:r=
,即:r= ;
;
②cosθ≠0时,由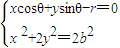 ,
,
得(1+cos2θ)y2-2rsinθy+r2-2b2cos2θ=0,
所以 ,
,
因为x1x2cos2θ=r2-(y1+y2)rsinθ+sin2θ,
由OQ1⊥OQ2得,x1x2cos2θ+y1y2cos2θ=r2-(y1+y2)rsinθ+y1y2=0
所以3r2cos2θ=2b2cos2θ,从而r= ;
;
由①、②知,r= .
.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,由此能够求出a=
,由此能够求出a= .
.(2)设MF1=m,MF2=n,m+n=2a,由余弦定理得
 =
= .因为
.因为 ,所以cos∠F1MF2≥0,由此能够证明:∠F1MF2的最大值为
,所以cos∠F1MF2≥0,由此能够证明:∠F1MF2的最大值为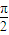 .
.(3)设G(rcosθ,rsinθ)圆上任意一点,过G点的切线交该椭圆于Q1(x1,x2),Q2(x2,y2),则切线l的法向量为(rcosθ,rsinθ),直线l的方程为xcosθ+ysinθ-r=0,联立方程组
 ,能够推导出r=
,能够推导出r= .
.解答:解:(1)设F1(-c,0),F2(c,0),A(a,c),B(0,b),
因为MF2⊥F1F2,所以点M坐标为
 ,
,所以MF1方程b2x-2axy+b2c=0,
O到MF1距离
 ,整理得2b4=a2c2,
,整理得2b4=a2c2,所以
 解得a=
解得a=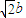 .
.(2)设MF1=m,MF2=n,m+n=2a,
由余弦定理得

=

=
 .
.因为
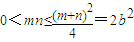 ,
,所以cos∠F1MF2≥0,
当且仅当m=n=a=
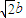 ,cos∠F1MF2=0,
,cos∠F1MF2=0,由三角形内角及余弦单调性知有最大值
 .
.(3)设G(rcosθ,rsinθ)圆上任意一点,过G点的切线交该椭圆于Q1(x1,x2),Q2(x2,y2),
则切线l的法向量为(rcosθ,rsinθ),直线l的方程为xcosθ+ysinθ-r=0,
联立方程组
 ,
,①cosθ=0时,|OG|=|Q1G|=|Q2G|,所以r=
 ,即:r=
,即:r= ;
;②cosθ≠0时,由
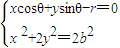 ,
,得(1+cos2θ)y2-2rsinθy+r2-2b2cos2θ=0,
所以
 ,
,因为x1x2cos2θ=r2-(y1+y2)rsinθ+sin2θ,
由OQ1⊥OQ2得,x1x2cos2θ+y1y2cos2θ=r2-(y1+y2)rsinθ+y1y2=0
所以3r2cos2θ=2b2cos2θ,从而r=
 ;
;由①、②知,r=
 .
.点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过顶点A、B的直线与原点的距离为
,过顶点A、B的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
. ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点.问:是否存在
两点.问:是否存在 的值,使以
的值,使以 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由.