题目内容
设椭圆T: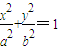 (a>b>0),直线l过椭圆左焦点F1且不与x轴重合,l与椭圆交于P、Q,当l与x轴垂直时,|PQ|=
(a>b>0),直线l过椭圆左焦点F1且不与x轴重合,l与椭圆交于P、Q,当l与x轴垂直时,|PQ|=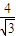 ,F2为椭圆的右焦点,M为椭圆T上任意一点,若△F1MF2面积的最大值为
,F2为椭圆的右焦点,M为椭圆T上任意一点,若△F1MF2面积的最大值为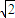 .
.(1)求椭圆T的方程;
(2)直线l绕着F1旋转,与圆O:x2+y2=5交于A、B两点,若|AB|∈(4,
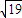 )),求△F2PQ的面积S的取值范围.
)),求△F2PQ的面积S的取值范围.
【答案】分析:(1)由题意可将x=-c代入椭圆方程可得,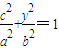 结合c=
结合c=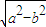 可得y=
可得y=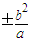 ,从而可求|PQ|,再由△F1MF2面积的最大值为
,从而可求|PQ|,再由△F1MF2面积的最大值为 可得
可得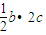 =
=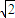 ,由方程可求a,b进而可求椭圆方程
,由方程可求a,b进而可求椭圆方程
(2)设直线L:x=my-1,可求圆心O到直线L的距离d,由圆的性质可知AB=2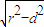 =
=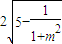
由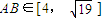 ,可求m的范围,联立方程组
,可求m的范围,联立方程组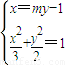 消去x,设P(x1,y1),Q(x2,y2),则根据方程的根与系数关系可得,
消去x,设P(x1,y1),Q(x2,y2),则根据方程的根与系数关系可得,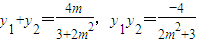 ,代入
,代入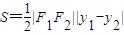 =
=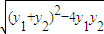 ,代入整理,结合函数的单调性可求S的范围
,代入整理,结合函数的单调性可求S的范围
解答:解:(1)由题意可将x=-c代入椭圆方程可得,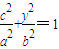
∵c=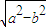
∴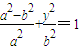 即y=
即y=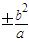
∴|PQ|=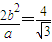 ①
①
由已知可得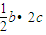 =
=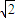 ②
②
①②联立可得a2=3,b2=2
∴椭圆的方程为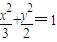
(2)设直线L:x=my-1即x-my+1=0,圆心O到直线L的距离d=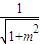
由圆的性质可知AB=2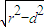 =
=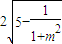
又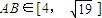 ,则
,则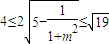
∴m2≤3
联立方程组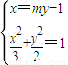 消去x可得(2m2+3)y2-4my-4=0
消去x可得(2m2+3)y2-4my-4=0
设P(x1,y1),Q(x2,y2),则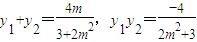
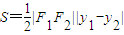 =
=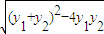 =
=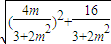
=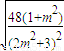 =
=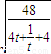 (令t=m2+1∈[1,4])
(令t=m2+1∈[1,4])
设f(t)=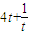 (t∈[1,4])
(t∈[1,4])
则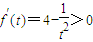 对一切t∈[1,4]恒成立
对一切t∈[1,4]恒成立
∴f(t)=4t+ 在[1,4]上单调递增,4t+
在[1,4]上单调递增,4t+
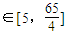
∴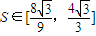
点评:本题主要考查了由椭圆的性质求解椭圆方程,点到直线的距离公式,圆的性质的应用,直线与圆锥曲线的相交关系的应用,还要具备一定的逻辑推理与运算的能力.
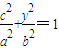 结合c=
结合c=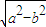 可得y=
可得y=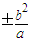 ,从而可求|PQ|,再由△F1MF2面积的最大值为
,从而可求|PQ|,再由△F1MF2面积的最大值为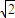 可得
可得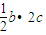 =
=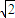 ,由方程可求a,b进而可求椭圆方程
,由方程可求a,b进而可求椭圆方程(2)设直线L:x=my-1,可求圆心O到直线L的距离d,由圆的性质可知AB=2
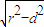 =
=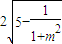
由
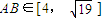 ,可求m的范围,联立方程组
,可求m的范围,联立方程组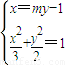 消去x,设P(x1,y1),Q(x2,y2),则根据方程的根与系数关系可得,
消去x,设P(x1,y1),Q(x2,y2),则根据方程的根与系数关系可得,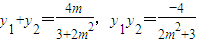 ,代入
,代入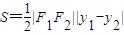 =
=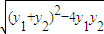 ,代入整理,结合函数的单调性可求S的范围
,代入整理,结合函数的单调性可求S的范围解答:解:(1)由题意可将x=-c代入椭圆方程可得,
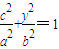
∵c=
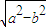
∴
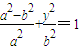 即y=
即y=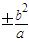
∴|PQ|=
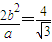 ①
①由已知可得
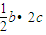 =
=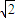 ②
②①②联立可得a2=3,b2=2
∴椭圆的方程为
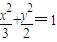
(2)设直线L:x=my-1即x-my+1=0,圆心O到直线L的距离d=
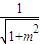
由圆的性质可知AB=2
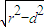 =
=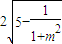
又
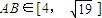 ,则
,则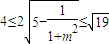
∴m2≤3
联立方程组
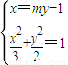 消去x可得(2m2+3)y2-4my-4=0
消去x可得(2m2+3)y2-4my-4=0设P(x1,y1),Q(x2,y2),则
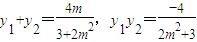
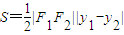 =
=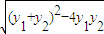 =
=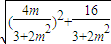
=
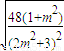 =
=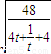 (令t=m2+1∈[1,4])
(令t=m2+1∈[1,4])设f(t)=
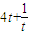 (t∈[1,4])
(t∈[1,4])则
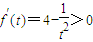 对一切t∈[1,4]恒成立
对一切t∈[1,4]恒成立∴f(t)=4t+
 在[1,4]上单调递增,4t+
在[1,4]上单调递增,4t+
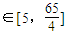
∴
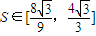
点评:本题主要考查了由椭圆的性质求解椭圆方程,点到直线的距离公式,圆的性质的应用,直线与圆锥曲线的相交关系的应用,还要具备一定的逻辑推理与运算的能力.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 (a>b>0)的一个顶点坐标为A(
(a>b>0)的一个顶点坐标为A(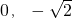 ),且其右焦点到直线
),且其右焦点到直线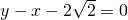 的距离为3.
的距离为3.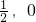 ),求证:点M的所有“相关弦”的中点在同一条直线上;
),求证:点M的所有“相关弦”的中点在同一条直线上;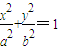 (a>b>0),直线l过椭圆左焦点F1且不与x轴重合,l与椭圆交于P、Q,当l与x轴垂直时,|PQ|=
(a>b>0),直线l过椭圆左焦点F1且不与x轴重合,l与椭圆交于P、Q,当l与x轴垂直时,|PQ|=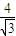 ,F2为椭圆的右焦点,M为椭圆T上任意一点,若△F1MF2面积的最大值为
,F2为椭圆的右焦点,M为椭圆T上任意一点,若△F1MF2面积的最大值为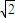 .
. )),求△F2PQ的面积S的取值范围.
)),求△F2PQ的面积S的取值范围.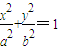 (a>b>0)的一个顶点坐标为A(
(a>b>0)的一个顶点坐标为A(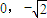 ),且其右焦点到直线
),且其右焦点到直线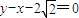 的距离为3.
的距离为3.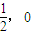 ),求证:点M的所有“相关弦”的中点在同一条直线上;
),求证:点M的所有“相关弦”的中点在同一条直线上;