题目内容
已知函数f(x)=ax-lnx(a>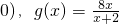 .
.
(I)求证f(x)≥1+lna;
(II)若对任意的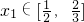 ,总存在唯一的
,总存在唯一的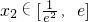 (e为自然对数的底数),使得g(x1)=f(x2),求实数a的取值范围.
(e为自然对数的底数),使得g(x1)=f(x2),求实数a的取值范围.
(I)证明:求导数可得f′(x)=a- (x>0)
(x>0)
令f′(x)>0,可得x> ,令f′(x)<0,可得0<x<
,令f′(x)<0,可得0<x<
∴x= 时,函数取得最小值
时,函数取得最小值
∴f(x)≥f( )=1+lna;
)=1+lna;
(II)解:g′(x)=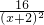 >0,∴函数g(x),当
>0,∴函数g(x),当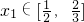 时,函数为增函数,∴g(x)∈[
时,函数为增函数,∴g(x)∈[ ,2]
,2]
当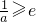 时,函数f(x)在
时,函数f(x)在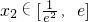 上单调减,∴f(x)∈[
上单调减,∴f(x)∈[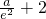 ,ae-1]
,ae-1]
∴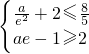 ,无解;
,无解;
当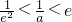 时,函数f(x)在
时,函数f(x)在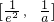 上单调减,在
上单调减,在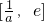 上单调增,f(
上单调增,f( )=1+lna≤
)=1+lna≤ ,∴a≤
,∴a≤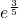 ,∴
,∴ <a≤
<a≤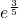
当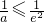 时,函数f(x)在
时,函数f(x)在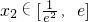 上单调增,∴f(x)∈[
上单调增,∴f(x)∈[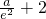 ,ae-1],∴
,ae-1],∴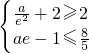 ,无解
,无解
综上知, <a≤
<a≤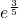 .
.
分析:(I)求导数,由导数的正负取得函数的单调性,从而可得函数的最值,即可证明结论;
(II)首先确定g(x)∈[ ,2],再分类讨论确定函数f(x)的值域,利用对任意的
,2],再分类讨论确定函数f(x)的值域,利用对任意的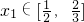 ,总存在唯一的
,总存在唯一的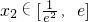 (e为自然对数的底数),使得g(x1)=f(x2),建立不等式,即可求实数a的取值范围.
(e为自然对数的底数),使得g(x1)=f(x2),建立不等式,即可求实数a的取值范围.
点评:本题考查的知识点是利用导数求闭区间上函数的最值,函数解析式的求解及常用方法,考查分类讨论的数学思想,属于中档题.
 (x>0)
(x>0)令f′(x)>0,可得x>
 ,令f′(x)<0,可得0<x<
,令f′(x)<0,可得0<x<
∴x=
 时,函数取得最小值
时,函数取得最小值∴f(x)≥f(
 )=1+lna;
)=1+lna;(II)解:g′(x)=
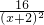 >0,∴函数g(x),当
>0,∴函数g(x),当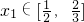 时,函数为增函数,∴g(x)∈[
时,函数为增函数,∴g(x)∈[ ,2]
,2]当
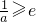 时,函数f(x)在
时,函数f(x)在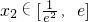 上单调减,∴f(x)∈[
上单调减,∴f(x)∈[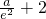 ,ae-1]
,ae-1]∴
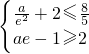 ,无解;
,无解;当
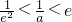 时,函数f(x)在
时,函数f(x)在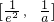 上单调减,在
上单调减,在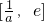 上单调增,f(
上单调增,f( )=1+lna≤
)=1+lna≤ ,∴a≤
,∴a≤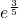 ,∴
,∴ <a≤
<a≤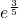
当
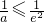 时,函数f(x)在
时,函数f(x)在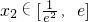 上单调增,∴f(x)∈[
上单调增,∴f(x)∈[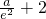 ,ae-1],∴
,ae-1],∴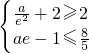 ,无解
,无解综上知,
 <a≤
<a≤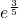 .
.分析:(I)求导数,由导数的正负取得函数的单调性,从而可得函数的最值,即可证明结论;
(II)首先确定g(x)∈[
 ,2],再分类讨论确定函数f(x)的值域,利用对任意的
,2],再分类讨论确定函数f(x)的值域,利用对任意的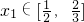 ,总存在唯一的
,总存在唯一的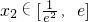 (e为自然对数的底数),使得g(x1)=f(x2),建立不等式,即可求实数a的取值范围.
(e为自然对数的底数),使得g(x1)=f(x2),建立不等式,即可求实数a的取值范围.点评:本题考查的知识点是利用导数求闭区间上函数的最值,函数解析式的求解及常用方法,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目