Question

函数f(x)=

1

2

(sinx+cosx)+

1

2

|sinx-cosx|的值域是（　　）

• A、[-1，1]
• B、[-

  2

  2

  ，1]
• C、[-

  1

  2

  ，

  1

  2

  ]
• D、[-1，

  2

  2

  ]

Answer 1

分析：根据绝对值内式子的符号分sinx≥cosx和cosx＞sinx两种情况，化简解析式并用分段函数表示，在根据函数图象求出每一部分的值域，最后在和在一起．

解答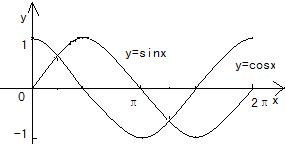：解：f(x)=

1

2

(sinx+cosx)+

1

2

|sinx-cosx|=

sinx   sinx≥cosx cosx   cosx＞sinx

，
 在坐标系中画出一个周期内y=sinx和y=cosx的图象：
由图得，当sinx≥cosx时，sinx∈[-

2

2

，1]；
当cosx＞sinx时，cosx（-

2

2

，1]，
∴原函数的值域是[-

2

2

，1]．
故选B．

点评：本题考查了由正弦（余弦）函数的图象求其它函数的值域，此题需要化简函数解析式，根据分段函数求值域的方法，即求出每个范围内的值域，最后再并在一起．