Question

【题目】已知a，b，c分别是△ABC内角A，B，C的对边，sin2B=2sinAsinC．
（Ⅰ）若a=b，求cosB；
（Ⅱ）设B=90°，且a= ， 求△ABC的面积．

Answer 1

【答案】解：（I）∵sin2B=2sinAsinC，
由正弦定理可得：＞0，
代入可得（bk）2=2akck，
∴b2=2ac，
∵a=b，∴a=2c，
由余弦定理可得：cosB===．
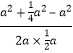（II）由（I）可得：b2=2ac，
∵B=90°，且a=，
∴a2+c2=2ac，解得a=c=．
∴S△ABC=ac=1．
【解析】（I）sin2B=2sinAsinC，由正弦定理可得：b2=2ac，再利用余弦定理即可得出．
（II）利用（I）及勾股定理可得c，再利用三角形面积计算公式即可得出．