题目内容
(本小题14分)
已知函数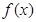 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义:
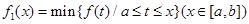 ,
, ,其中
,其中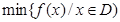 表示函数
表示函数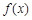 在D上的最小值,
在D上的最小值, 表示函数
表示函数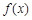 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得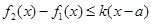 对任意的
对任意的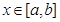 成立,则称函数
成立,则称函数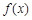 为
为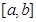 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若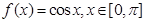 ,试写出
,试写出 ,
,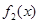 的表达式;
的表达式;
(2)已知函数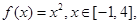 试判断
试判断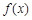 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知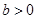 ,函数
,函数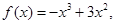 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
【答案】
解:(1)由题意可得: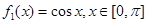 ,
,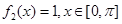 。
。
(2)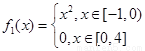 ,
,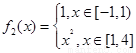 ,
,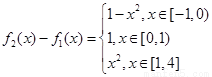
当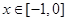 时,
时,
当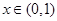 时,
时,
当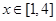 时,
时,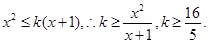
综上所述,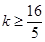 。
。
即存在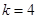 ,使得
,使得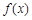 是[-1,4]上的“4阶收缩函数”。
是[-1,4]上的“4阶收缩函数”。
(3)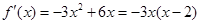 ,令
,令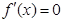 得
得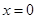 或
或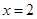 。
。
函数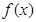 的变化情况如下:
的变化情况如下:
|
x |
|
0 |
|
2 |
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
0 |
|
4 |
|
令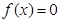 得
得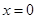 或
或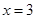 。
。
(i)当 时,
时,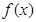 在
在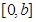 上单调递增,因此,
上单调递增,因此,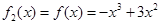 ,
,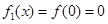 。因为
。因为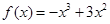 是
是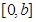 上的“二阶收缩函数”,所以,
上的“二阶收缩函数”,所以,
①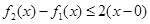 对
对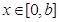 恒成立;
恒成立;
②存在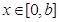 ,使得
,使得 成立。
成立。
①即: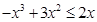 对
对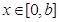 恒成立,由
恒成立,由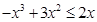 解得
解得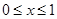 或
或 。
。
要使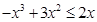 对
对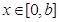 恒成立,需且只需
恒成立,需且只需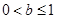 。
。
②即:存在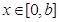 ,使得
,使得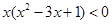 成立。
成立。
由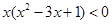 解得
解得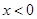 或
或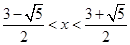 。
。
所以,只需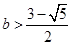 。
。
综合①②可得 。
。
(i i)当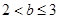 时,
时,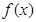 在
在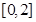 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
因此, ,
,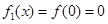 ,
, ,
,
显然当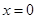 时,
时,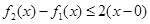 不成立。
不成立。
(i i i)当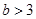 时,
时,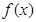 在
在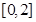 上单调递增,在
上单调递增,在 上单调递减,因此,
上单调递减,因此, ,
,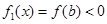 ,
,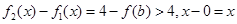 ,
,
显然当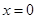 时,
时,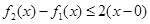 不成立。
不成立。
综合(i)(i i)(i i i)可得:
【解析】略

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
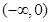
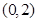
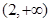
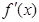
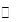
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中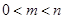 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间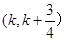 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
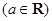 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意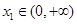 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。