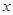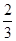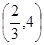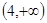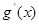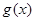题目内容
.(本小题满分12分)
函数 的图像如图所示。
的图像如图所示。

(1)若函数 在
在 处的切线方程为
处的切线方程为 求函数
求函数 的解析式
的解析式
(2)在(1)的条件下,是否存在实数 ,使得
,使得 的图像与
的图像与
的图像有且只有三个不同的交点?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
【答案】
解:(1)由图可知函数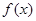 的图像过点(0,3),且
的图像过点(0,3),且
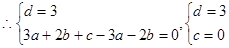 ————3
————3
依题意 ,解得
,解得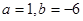
所以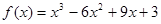 ————6
————6
(2)由题意可得: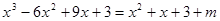 有三个不相等的实根,
有三个不相等的实根,
即 与
与 有三个不同的交点
有三个不同的交点
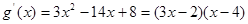
|
|
|
|
|
4 |
|
|
|
+ |
0 |
_ |
0 |
+ |
|
|
增 |
极大 |
减 |
极小 |
增 |
则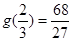 ,
,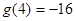 ,故
,故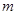 的取值范围是
的取值范围是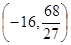 ————12
————12
【解析】略

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目