题目内容
(本小题满分12分)已知函数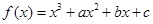 ,曲线
,曲线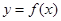 在
在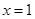
处的切线为l: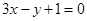 .
.
(1)若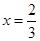 时,函数
时,函数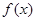 有极值,求函数
有极值,求函数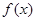 的解析式;
的解析式;
(2)若函数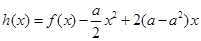 ,求
,求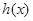 的单调递增区间(其中
的单调递增区间(其中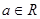 ).
).
【答案】
解:(1)由f(x)=x3+ax2+bx+c,得
f′(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0. ①
当x=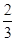 时,y=f(x)有极值,则f′
时,y=f(x)有极值,则f′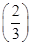 =0,
=0,
可得4a+3b+4=0. ②
由①、②解得a=2,b=-4.
由于l上的切点的横坐标为x=1,
∴f(1)=4. ∴1+a+b+c=4.
∴c=5.
则f(x)=x3+2x2-4x+5. …………………6分
(2)由(1)得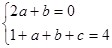 ,
,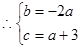 ,
,
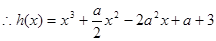 .
.
则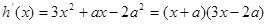 .
.
①当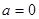 时,
时,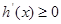 恒成立,
恒成立,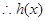 在R上单调递增;
在R上单调递增;
②当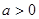 时,令
时,令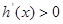 ,解得
,解得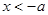 或
或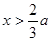 ,
,
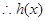 的单调递增区间是
的单调递增区间是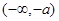 和
和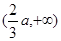 ;
;
③当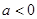 时,令
时,令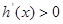 ,解得
,解得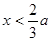 或
或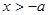
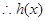 的单调递增区间是
的单调递增区间是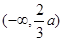 和
和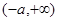 .
……………………12分
.
……………………12分
【解析】略

练习册系列答案
相关题目