题目内容
已知 为
为 的内角
的内角 的对边,满足
的对边,满足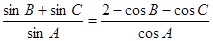 ,函数
,函数
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,证明
,证明 为等边三角形.
为等边三角形.
 为
为 的内角
的内角 的对边,满足
的对边,满足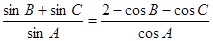 ,函数
,函数
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.(Ⅰ)证明:
 ;
;(Ⅱ)若
 ,证明
,证明 为等边三角形.
为等边三角形.(1)根据正弦定理和两角和差关系的运用来得到证明。
(2)根据余弦定理得到三边长度相等来得到结论。
(2)根据余弦定理得到三边长度相等来得到结论。
试题分析:解:(Ⅰ)根据题意,由于
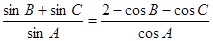 ,根据正弦定理,可知
,根据正弦定理,可知 ,
,故可知

(Ⅱ)由题意知:由题意知:
 ,解得:
,解得: , 8分
, 8分因为
 ,
, 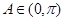 ,所以
,所以 9分
9分由余弦定理知:
 10分
10分所以
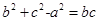 因为
因为 ,所以
,所以 ,
,即:
 所以
所以 11分
11分又
 ,所以
,所以 为等边三角形. 12分
为等边三角形. 12分点评:主要是考查了解三角形的运用,属于基础题。

练习册系列答案
相关题目
 .
. 最大值和最小正周期;
最大值和最小正周期; 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,若
,若 ,求
,求 的值
的值 )=
)=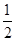 ,则sinθ+cosθ=_________.
,则sinθ+cosθ=_________. ( )
( )



 △ABC中,
△ABC中, ,则
,则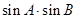 的最大值是_____________
的最大值是_____________  ,
,  , 则
, 则 的值为_________。
的值为_________。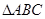 中,
中, 为锐角,角
为锐角,角 所对的边分别为
所对的边分别为 ,且
,且
 的值;
的值; ,求
,求 ,
,
 中,角
中,角 的对边
的对边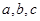 满足:
满足: ,给出下列不等式:
,给出下列不等式: ;②
;② ;③
;③ .
.