题目内容
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在 如图所示的三棱台6个顶点 ,
, ,
, ,
, ,
, ,
, 上 各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有
种(用数字作答).
上 各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有
种(用数字作答).

【答案】
264
【解析】解:∵至少用了三种颜色的灯泡安装.
∴可能用了三种颜色安装,可能用了四种颜色安装.
由分类计数原理,可分两类:
第一类,用了三种颜色安装,
第一步,为A、B、C三点选三种颜色灯泡共有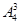 种选法;第二步,为A1点选一种颜色共有不同于A点的2种选法;第三步,为B1、C1选灯泡,共有1种选法
种选法;第二步,为A1点选一种颜色共有不同于A点的2种选法;第三步,为B1、C1选灯泡,共有1种选法
∴第一类共有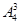 ×2×1=48种方法.
×2×1=48种方法.
第二类,用了四种颜色安装,
第一步,为A、B、C三点选三种颜色灯泡共有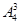 种选法;第二步,为A1点选一种颜色共有不同于A点的3种选法;第三步,为B1、C1选灯泡:若B1与A同色,则C1只能选B点颜色;若B1与C同色,则C1有A、B处两种颜色可选.故为B1、C1选灯泡共有3种选法
种选法;第二步,为A1点选一种颜色共有不同于A点的3种选法;第三步,为B1、C1选灯泡:若B1与A同色,则C1只能选B点颜色;若B1与C同色,则C1有A、B处两种颜色可选.故为B1、C1选灯泡共有3种选法
∴第二类共有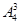 ×3×3=216种方法.
×3×3=216种方法.
综上所述,至少用了三种颜色的灯泡的安装方法共有48+216=264种方法
故答案为 264

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 16、某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有
16、某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有 某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有( )种.
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有( )种. 某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )