题目内容
已知数列![]() 中,
中,![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足
![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
解:(1)由已知,![]() (
(![]() ,
,![]() ),
),
即![]() (
(![]() ,
,![]() ),且
),且![]() .
.
∴数列![]() 是以
是以![]() 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴![]() .
.
(2)∵![]() ,∴
,∴![]() ,要使
,要使![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
∴![]() 恒成立.
恒成立.
()当![]() 为奇数时,即
为奇数时,即![]() 恒成立,
恒成立,
当且仅当![]() 时,
时,![]() 有最小值为1,
有最小值为1,
∴![]() .
.
()当![]() 为偶数时,即
为偶数时,即![]() 恒成立,
恒成立,
当且仅当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
∴![]() .
.
即![]() ,又
,又![]() 为非零整数,则
为非零整数,则![]() .
.
综上所述,存在![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() .
.

练习册系列答案
相关题目
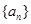 中,
中,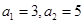 ,
,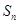 为其前n项和,且满足
为其前n项和,且满足
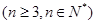 。
。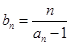 ,求数列
,求数列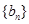 的前n项和
的前n项和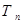 ;
;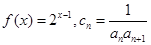 ,
,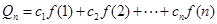 ,求证
,求证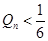 (n∈N*)。
(n∈N*)。