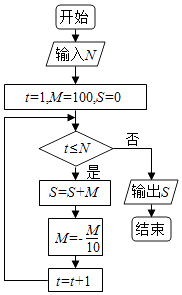
题目内容
【题目】已知函数 ![]() ,
, ![]() .
.
(Ⅰ)当 ![]() 在
在 ![]() 处的切线与直线
处的切线与直线 ![]() 垂直时,方程
垂直时,方程 ![]() 有两相异实数根,求
有两相异实数根,求 ![]() 的取值范围;
的取值范围;
(Ⅱ)若幂函数 ![]() 的图象关于
的图象关于 ![]() 轴对称,求使不等式
轴对称,求使不等式 ![]() 在
在 ![]() 上恒成立的
上恒成立的 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)由题设可得 ![]() ,令
,令 ![]() ,
,
则 ![]() 令
令 ![]() 得
得 ![]() ,
,
|
|
|
|
|
| 0 |
|
| 递减 | 极小值 | 递增 |
![]() ,
,
且 ![]() 有两个不等实根
有两个不等实根 ![]() 即
即 ![]()
![]() .
.
(Ⅱ)由题设有 ![]() ,令
,令 ![]() ,
,
则 ![]() ,令
,令 ![]() ,则
,则![]() 又
又 ![]() ,
, ![]() ,
, ![]() 在
在 ![]() 在单调递增,
在单调递增,
又 ![]() ,
,
当 ![]() ,即
,即 ![]() 时,
时, ![]() ,
,
所以 ![]() 在
在 ![]() 内单调递增,
内单调递增, ![]() ,所以
,所以 ![]() .
.
②当 ![]() ,即
,即 ![]() 时,由
时,由 ![]() 在
在 ![]() 内单调递增,
内单调递增,
且 ![]() ,
,![]() 使得
使得 ![]() ,
,
|
|
|
|
|
| 0 |
|
| 递减 | 极小值 | 递增 |
所以 ![]() 的最小值为
的最小值为 ![]() ,
,
又 ![]() ,所以
,所以 ![]()
![]() ,
,
因此,要使当 ![]() 时,
时, ![]() 恒成立,只需
恒成立,只需 ![]() ,即
,即 ![]() 即可.
即可.
解得 ![]() ,此时由
,此时由 ![]() ,可得
,可得 ![]() .
.
以下求出a的取值范围.
设 ![]() ,
, ![]() , 得
, 得 ![]() ,
,
所以 ![]() 在
在 ![]() 上单调递减,从而
上单调递减,从而 ![]() ,
,
综上①②所述, ![]() 的取值范围
的取值范围 ![]()
【解析】(1)方程f(x) = g(x) 有两相异的实数根等价于φ ( x ) = g ( x ) f ( x )由两个零点。(2)令t ( x ) = g ( x ) f ( x ),求出t ( x ) 的导函数利用导函数的性质对a分情况讨论进而研究出函数的单调性从而确定出函数的最值进而得到a的取值范围。
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数
在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.