题目内容
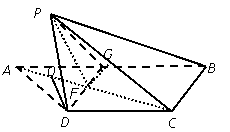
如图，梯形ABCD中，CD//AB
，E是AB的中点，将△ADE沿DE折起，
使点A折到点P的位置，且二面角
的大小为1200．
（I）求证：
；
（II）求直线PD与平面BCDE所成角的大小；
（III）求点D到平面PBC的距离.
解析：（I）连结AC交DE于F，连结PF．
，
．
又
，
，
，
即CA平分
． …………2分
是正三角形，
，即PF⊥DE，CF⊥DE，
∴DE⊥面PCF，∴DE⊥PC． …………4分
（II）过P作
于O，连结OD，设AD = DC = CB = a，则AB = 2a，
∵DE⊥面PCF，∴DE⊥PO，
∴PO⊥面BCDE，
∴∠PDO就是直线PD与平面BCDE所成的角． …………6分
∵∠PFC是二面角P-DE-C的平面角，
∴∠PFO = 60°，在RT△POD中，
，
E |
直线PD与平面BCDE所成角是
．……… …8分
（III）∵DE∥BC，DE在平面PBC外，
，
点到面
的距离即为点F到面PBC的距离，过点F作FG⊥PC，垂足为G．
∴DE⊥面PCF，
．
，
，
∴FG的长即为点F到面PBC的距离． …………10分
在菱形ADCE中，
，
．
，
，
． …………12分
练习册系列答案
阅读快车系列答案
相关题目
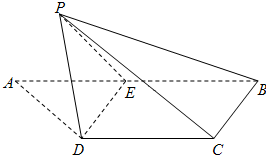如图，梯形ABCD中，CD∥AB，AD=DC=CB=
如图，梯形ABCD中，AD∥BC，PA⊥平面ABCD，E是PD的中点，AB=BC=1，PA=AD=2．
如图，梯形ABCD中，CD∥AB，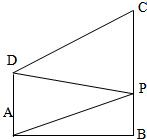
如图，梯形ABCD中，AD∥BC，AD⊥AB，AD=1，BC=2，AB=3，P是BC上的动点，当
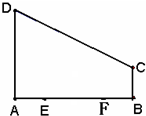如图直角梯形ABCD中，∠DAB=90°，AD∥BC，E，F是AB边的四等分点，AB=4，BC=BF=AE=1，AD=3，P为在梯形区域内一动点，满足PE+PF=AB，记动点P的轨迹为Γ．