题目内容
如果一个圆柱、一个圆锥的底面直径和高都等于一个球的直径,则圆柱、球、圆锥的体积之比依次是( )
| A、6:5:4 | B、5:4:3 | C、3:2:1 | D、4:2:1 |
分析:圆柱、圆锥、球的体积公式分别为V圆柱=S•h,V圆锥=
S•h,V球=
πR3,本题中可设球的半径为R,则圆柱的底面半径为R,高为2R;圆锥的底面半径为R,高为2R,于是代入上面的公式可得结果.
| 1 |
| 3 |
| 4 |
| 3 |
解答:解:设圆柱、圆锥的底面直径和高为2R,则球的直径也为2R,于是有:V圆柱=πR2•2R=2πR3,V圆锥=
πR22R=
πR3,V球=
πR3,
所以V圆柱:V球:V圆锥=(2πR3):(
πR3):(
πR3)=3:2:1.
故选C
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
所以V圆柱:V球:V圆锥=(2πR3):(
| 4 |
| 3 |
| 2 |
| 3 |
故选C
点评:本题考查了空间几何体中旋转体的结构特征,几何体圆柱,圆锥,球的体积计算公式.考查记忆能力,基本计算能力.

练习册系列答案
相关题目
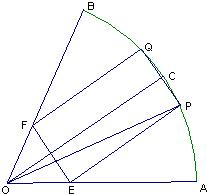 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.