题目内容
【题目】在直角坐标系xOy中，以O为原点，Ox轴为极轴，单位长度不变，建立极坐标系，直线l的极坐标方程为：ρsin（θ+ 
）= 
，曲线C的参数方程为： 
（1）写出直线l和曲线C的普通方程；
（2）若直线l和曲线C相交于A，B两点，定点P（﹣1，2），求线段|AB|和|PA||PB|的值．
【答案】
（1）解：直线l的极坐标方程为：ρsin（θ+ 
）= 
，
展开可得： ρ（sinθ+cosθ）= ，可得直角坐标方程：x+y﹣1=0．
曲线C的参数方程为： 
，x2=4（1+sin2t）=y，x∈ 
（2）解：直线l的参数方程为：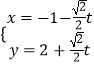 
，代入曲线C的方程可得： 
t﹣2=0，
∴t1+t2=﹣ 
，t1t2=﹣2．
∴|AB|=|t1﹣t2|= 
= 
= 
，
|PA||PB|=|t1t2|=2
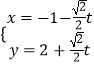【解析】（1）直线l的极坐标方程为：ρsin（θ+ ）= ，展开可得： ρ（sinθ+cosθ）= ，利用互化公式可得直角坐标方程．曲线C的参数方程为： ，可得x2=4（1+sin2t）=y，x∈ ．（2）直线l的参数方程为： ，代入曲线C的方程可得： t﹣2=0，可得|AB|=|t1﹣t2|= ，
|PA||PB|=|t1t2|．
【题目】已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示，下列关于函数f（x）的命题：
x | ﹣1 | 0 | 4 | 5 |
f（x） | 1 | 2 | 2 | 1 |
（1）函数y=f（x）是周期函数；
（2）函数f（x）在（0，2）上是减函数；
（3）如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；
（4）当1＜a＜2时，函数y=f（x）﹣a有4个零点．
其中真命题的个数有（ ）
A.1个
B.2个
C.3个
D.4个
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
