Question

已知奇函数y＝f(x)的定义域为(－∞，＋∞)，且满足条件：①当x＞0时，f(x)＜0；②对于任意实数x、y都有f(x＋y)＝f(x)＋f(y)．

(1)根据函数单调性的定义，证明y＝f(x)是减函数；

(2)若x＞0时不等式f(ax－2)＋f(x－x²)＞0恒成立，求实数a的取值范围．

Answer 1

答案：
解析：

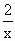(1)证明：设－∞＜x1＜x2＜＋∞，则x2－x1＞0．由条件①，有f(x2－x1)＜0．　　∵f(x)是奇函数，∴－f(x1)＝f(－x1)． 　　由条件②，有f(x2)＋f(－x1)＝f(x2－x1)． 　　∴f(x2)－f(x1)＝f(x2)＋f(－x1)＝f(x2－x1)＜0． 　　∴f(x2)＜f(x1)．　　∴f(x)在定义域上是减函数． 　　(2)解：由条件②，令x＝y＝0，则有 　　f(0＋0)＝f(0)＋f(0)，∴f(0)＝0． 　　对x＞0时不等式f(ax－2)＋f(x－x2)＞0恒成立即是 　　f(ax－2＋x－x2)＞0＝f(0)恒成立． 　　又∵f(x)是减函数，∴ax－2＋x－x2＜0在x＞0时恒成立． 　　∴ax＜x2＋2－x(x＞0)　　∴a＜x＋－1对于x＞0恒成立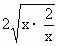． 　　∴a应小于函数y＝x＋－1(x＞0)的最小值． 　　而y＝x＋－1≥－1＝－1，当x＝时取得最小值． 　　∴a＜－1．　　∴a的取值范围为(－∞，－1)．