题目内容
(07年福建卷文)(本小题满分12分)
数列{an}的前N项和为Sn,a1=1,an+1=2Sn (n∈N*).
(I)求数列{an}的通项an;
(II)求数列{nan}的前n项和 Tn .
本小题考查数列的基本知识,考查等比数列的概念、通项公式及数列的求和,考查分类讨论及归的数学思想方法,以及推理和运算能力.满分12分.
解析:(I)∵an+1=2Sn,,
∴Sn+1-Sn=2Sn,
∴![]() =3.
=3.
又∵S1=a1=1,
∴数列{Sn}是首项为1、公比为3的等比数列,Sn=3n-1(n∈N*).
∴当n![]() 2时,an-2Sn-1=2?3n-2(n
2时,an-2Sn-1=2?3n-2(n![]() 2),
2),
∴an=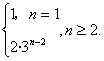
![]()
(II)Tn=a1+2a2+3a3+…+nan.
当n=1时,T1=1;
当n![]() 2时,Tn=1+4?30+6?31+2n?3 n-2,…………①
2时,Tn=1+4?30+6?31+2n?3 n-2,…………①
3Tn=3+4?31+6?32+…+2n?3n-1,…………②
①-②得:-2Tn=-2+4+2(31+32+…+3n-2)-2n?3 n-1
=2+2?![]()
=-1+(1-2n)?3n-1
∴Tn=![]() +(n-
+(n-![]() )3n-1 (n
)3n-1 (n![]() 2).
2).
又∵Tn=a1=1也满足上式,
∴Tn=![]() +(n-
+(n-![]() )3n-1(n∈N*)
)3n-1(n∈N*)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
