Question

（07年福建卷文）（本小题满分12分）

如图，正三棱柱ABC-A₁B₁C₁的所有棱长都为2，D为CC₁中点.

(I)求证：AB₁⊥平面A₁BD;

(II)求二面角A-A₁D-B的大小.

Answer 1

本小题主要考查直线与平面的位置关系，三面角的大小等知识，考查空间想象能力、逻辑思维能力和运算能力

解析：解法一：（I）取BC中点O，连结AO.

∵△ABC为正三角形，∴AO⊥BC.

∵正三棱柱ABC-A₁B₁C₁中，平面ABC⊥平面BCC₁B_1,

∴AO⊥平面BCC₁B₁,

连结B₁O，在正方形BB₁C₁C中,O、D分别为BC、CC₁的中点，

∴B₁O⊥BD,

∴AB₁⊥BD.

在正方形ABB₁A₁中，AB₁⊥A₁B，

∴AB₁⊥平面A₁BD.

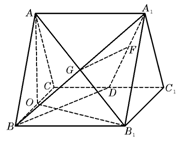
 (II)设AB₁与A₁B交于点C，在平面A₁BD中，作GF⊥A₁D于F，连结AF，由（I）得AB₁⊥平面A₁BD，

∴∠AFG为二面A-A₁B-B的平面角.

在△AA₁D中，由等面积法可求得AF＝，

又∵AG＝=,

∴sin∠AFG=,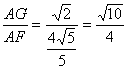

所以二面角A-A₁D-B的大小为arcsin.

解法二：

 

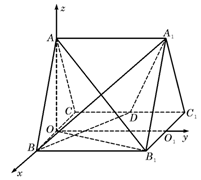
（I）取BC中点O，连结AO.

 

∵△ABC为正三角形，∴AO⊥BC.

∵正三棱柱ABC-A₁B₁C₁中，平面ABC⊥平面BCC₁B₁，

∴AO⊥平面BCC₁B₁.

取B₁C₁中点O₁，以a为原点，的方向为x、y、z轴的正方向建立空间直角坐标系，则B（1,0,0）,D (-1,1,0),A₁(0,2,),A(0,0,),B₁(1,2,0),

∴

∵

∴⊥⊥,

∴AB₁⊥平面A₁BD.

(II)设平面A₁AD的法向量为n=(x,y,z).

∵n⊥⊥,

∴    ∵   ∴

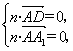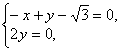令z=1得a=(-,0,1)为平面A₁AD的一个法向量.

由（I）知AB₁⊥A₁BD.

∴为平面A₁BD的法向量.

cos<n₁>===-.

∴二面角A-A₁D-B的大小为arccos.