题目内容
设椭圆C: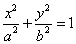 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为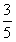 ,
,
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为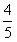 的直线被C所截线段的中点坐标。
的直线被C所截线段的中点坐标。
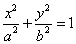 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为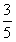 ,
,(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为
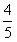 的直线被C所截线段的中点坐标。
的直线被C所截线段的中点坐标。解:(Ⅰ)将(0,4)代入C的方程得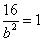
∴b=4
又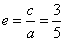
得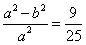 ,即
,即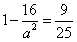
∴a=5
∴C的方程为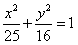 ;
;
(Ⅱ)过点且斜率为 的直线方程为
的直线方程为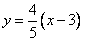
设直线与C的交点为A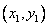 ,B
,B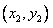
将直线方程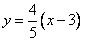 代入C的方程,得
代入C的方程,得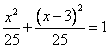
即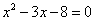 ,解得
,解得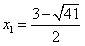 ,
,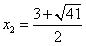
∴AB的中点坐标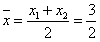 ,
,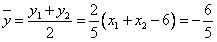
即中点为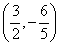 。
。
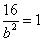
∴b=4
又
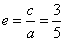
得
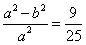 ,即
,即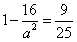
∴a=5
∴C的方程为
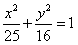 ;
;(Ⅱ)过点且斜率为
 的直线方程为
的直线方程为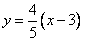
设直线与C的交点为A
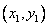 ,B
,B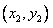
将直线方程
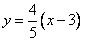 代入C的方程,得
代入C的方程,得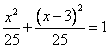
即
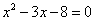 ,解得
,解得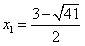 ,
,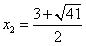
∴AB的中点坐标
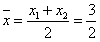 ,
,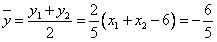
即中点为
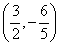 。
。
练习册系列答案
相关题目
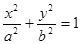 (a>b>0)的左、右焦点分别为F1、F2,P是C上的点,
(a>b>0)的左、右焦点分别为F1、F2,P是C上的点, ,
,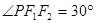 ,则C的离心率为( )
,则C的离心率为( )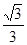 B.
B.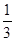 C.
C. D.
D.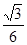
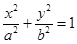 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为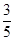
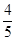 的直线被椭圆C所截线段的中点坐标。
的直线被椭圆C所截线段的中点坐标。 (a>b>0) 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0) 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 ,
,  相切,求椭圆C的方程:
相切,求椭圆C的方程: 
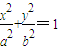 (a>b>0)的一个顶点坐标为A(
(a>b>0)的一个顶点坐标为A(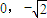 ),且其右焦点到直线
),且其右焦点到直线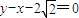 的距离为3.
的距离为3.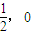 ),求证:点M的所有“相关弦”的中点在同一条直线上;
),求证:点M的所有“相关弦”的中点在同一条直线上;