题目内容
设α∈（0，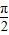
），方程
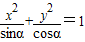表示焦点在x轴上的椭圆，则α∈（ ）A．（0，
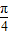]B．（
，
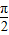）C．（0，
）D．[
，
）
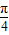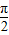【答案】分析：先根据椭圆焦点在x轴上得出sinα＞cosα，然后使cosα=sin（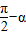 
）进而根据正弦函数的单调性求出α的取值范围．
解答：解：∵焦点在x轴上，
∴sinα＞cosα，
即sinα＞sin（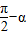
）
∵0＜α＜
∴α＞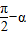
，即 
故选B．
点评：本题主要考查了椭圆的标准方程的问题．即对于椭圆标准方程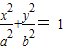
，当焦点在x轴上时，a＞b；当焦点在y轴上时，a＜b．
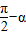）进而根据正弦函数的单调性求出α的取值范围．解答：解：∵焦点在x轴上，
∴sinα＞cosα，
即sinα＞sin（
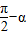）∵0＜α＜
∴α＞
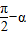，即 故选B．
点评：本题主要考查了椭圆的标准方程的问题．即对于椭圆标准方程
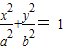，当焦点在x轴上时，a＞b；当焦点在y轴上时，a＜b． 
练习册系列答案
相关题目
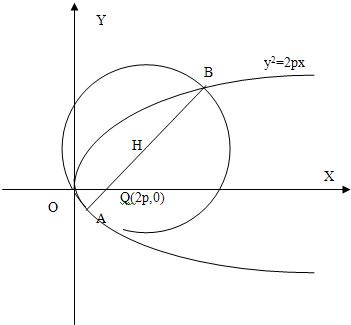设p＞0是一常数，过点Q（2p，0）的直线与抛物线y2=2px交于相异两点A、B，以线段AB为直经作圆H（H为圆心）．试证抛物线顶点在圆H的圆周上；并求圆H的面积最小时直线AB的方程．
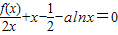的解的个数，并说明理由．