Question

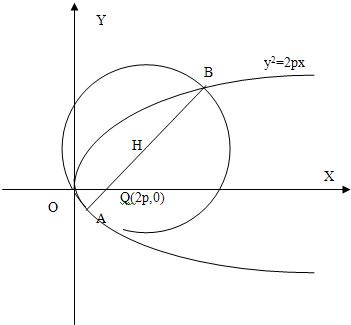设p＞0是一常数，过点Q（2p，0）的直线与抛物线y²=2px交于相异两点A、B，以线段AB为直经作圆H（H为圆心）．试证抛物线顶点在圆H的圆周上；并求圆H的面积最小时直线AB的方程．

Answer 1

分析：先设出A，B的坐标，把直线与抛物线方程联立消去x，根据韦达定理可分别求得y₁+y₂和y₁y₂及x₁+x₂和x₁x₂的从而求得

OA

•

OB

的值，结果为0，可推断出OA⊥OB，进而可知O必在圆H的圆周上，又根据H是AB的中点，进而可表示出圆心的坐标，求得|OH|的表达式，进而根据二次函数的性质求得|OH|即圆的半径的最小值，即进而可知当a=0时，圆的面积最小．

解答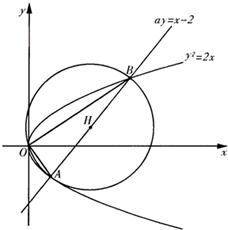：解：由题意，设直线AB的方程为ay=x-2，
设A（x₁，y₁），B（x₂，y₂），则其坐标满足

ay=x-2 y2=2px

消去x的y²-2apy-4p²=0，
则

x1+x2=(4+2a2)p x1•x2=4p2

因此

OA

•

OB

=x₁x₂+y₁y₂=0
∴OA⊥OB，故O必在圆H的圆周上，
又由题意圆心H是AB的中点，故

xH=(2+a2)p yH=ap

，
由前已证OH应是圆H的半径，且|OH|=

a4+5a2+4

p；
从而当a=0时，圆H的半径最小，也使圆H的面积最小．

点评：本题主要考查了抛物线的应用．考查了考生运用所学知识解决实际问题的能力．