题目内容

如图，已知三棱锥P—ABC的三条侧棱两两垂直，P在底面ABC内的射影为H，求证：△APB的面积是△ABC和△AHB的面积的比例中项.

证明:∵PA、PB、PC两两垂直，∴H为△ABC的垂心.连结CH并延长交AB于D，连结PD，由三垂线定理知PD⊥AB.

由条件知，PC⊥面ABP，∴PC⊥PD.

在Rt△CPD中，由射影定理，得PD2=CD·HD.

∴AB2·PD2=AB·CD·AB·HD，

即S△APB2=S△ABC·S△AHB.

练习册系列答案
相关题目
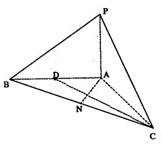精英家教网如图，已知三棱锥P-ABC中，PA⊥平面ABC，AN⊥BC于N，D是AB的中点，且PA=1，AN=BN=CN=
2
．
（1）求证：PB⊥AC；
（2）求异面直线CD与PB所成角的大小；
（3）求点A到平面PBC的距离．
如图，已知三棱锥P-ABC中，PA⊥面ABC，其中正视图为Rt△PAC，AC=2
6
，PA=4，俯视图也为直角三角形，另一直角边长为2
2
．
（1）画出侧视图并求侧视图的面积；
（2）求三棱锥P-ABC体积．
如图，已知三棱锥P-ABC的侧面PAB是等边三角形，D是AB的中点，PC=BC=AC=2，PB=2
2
．
（1）证明：AB⊥平面PCD；
（2）求点C到平面PAB的距离．
如图，已知三棱锥P-ABC，∠ACB=90°，CB=4，AB=20，D为AB中点，M为PB的中点，且△PDB是正三角形，PA⊥PC．
（I）求证：DM∥平面PAC；
（II）求证：平面PAC⊥平面ABC；
（Ⅲ）求三棱锥M-BCD的体积．
（2009•河西区二模）如图，已知三棱锥P-ABC中，底面△ABC是边长为4
2
的等边三角形，又PA=PB=2
6
，PC=2
10

（I）证明平面PAB⊥平面ABC；
（Ⅱ）求直线PB与平面PAC所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网