题目内容
已知抛物线![]() 的焦点为F,以点A(
的焦点为F,以点A(![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆在x轴的上方与抛物线交于M、N两点。
为半径的圆在x轴的上方与抛物线交于M、N两点。
(1)求证:点A在以M、N为焦点,且过F的椭圆上。
(2)设点P为MN的中点,是否存在这样的a,使得解析:(1)因为 点A的坐标为(![]() ,0),抛物线
,0),抛物线![]() 的焦点为F(a,0),准线为
的焦点为F(a,0),准线为![]() ,
,
所以 ![]()
所以 以A为圆心,|FA| 为半径的圆在x轴的上方的方程为
![]() ,(
,(![]() )
)
由
得 ![]()
设M(![]() ),N(
),N(![]() )(其中:
)(其中:![]() (
(![]() )均为正数),则有
)均为正数),则有
![]()

又 抛物线上的点到焦点与准线的距离相等
所以 ![]()

![]()
因为点F、M、N均在⊙A上,
所以![]() ,
,
![]()
因为![]() ,且
,且![]()
所以点A在以M、N为焦点且过F的椭圆上
(2)假设存在满足条件的a,则有
![]() ,即
,即![]()
设点P的坐标为(![]() ),则有
),则有

由![]() ,得
,得
![]()
化简,得![]()
所以![]() ,与
,与![]() 矛盾
矛盾
故不存在满足条件的![]() ,即不存在
,即不存在![]() 值,使得点P为MN的中点,且|FP|是|FM|与|FN|的等差中项。
值,使得点P为MN的中点,且|FP|是|FM|与|FN|的等差中项。

练习册系列答案
相关题目
 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.
 的最小值.
的最小值. 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为 ,过P点作平行于
,过P点作平行于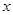 轴的直线
轴的直线 ,过焦点F作平行于
,过焦点F作平行于 ,则点P的坐标为 。
,则点P的坐标为 。 的焦点为F,过点F作直线
的焦点为F,过点F作直线 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与 轴交于点C。
轴交于点C。 ;
; 的最大值,并求
的最大值,并求 的焦点为F,过点
的焦点为F,过点 的直线
的直线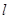 与
与 相交于
相交于 、
、 两点,点A关于
两点,点A关于 轴的对称点为D .
轴的对称点为D . ,求
,求 的内切圆M的方程 .
的内切圆M的方程 . 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在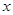 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8