题目内容
如图,已知抛物线 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.

(1)求证:KF平分∠MKN;
(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求 的最小值.
的最小值.
【答案】
(1)见解析;(2)8.
【解析】
试题分析:(1)只需证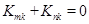 ,设出M,N两点坐标和直线MN方程,再把直线方程与抛物线方程联立,由韦达定理可得证;(2)由(1)设出的M,N两点坐标分别先求出P、Q两点坐标,还是把设出的直线MN方程与抛物线方程联立,由韦达定理把
,设出M,N两点坐标和直线MN方程,再把直线方程与抛物线方程联立,由韦达定理可得证;(2)由(1)设出的M,N两点坐标分别先求出P、Q两点坐标,还是把设出的直线MN方程与抛物线方程联立,由韦达定理把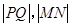 表示出来,再根据直线MN的倾斜角的范围求
表示出来,再根据直线MN的倾斜角的范围求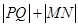 的最小值.
的最小值.
试题解析:(1)抛物线焦点坐标为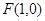 ,准线方程为
,准线方程为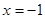 . 2分
. 2分
设直线MN的方程为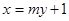 。设M、N的坐标分别为
。设M、N的坐标分别为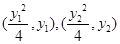
由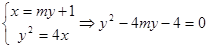 , ∴
, ∴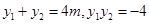 .
4分
.
4分
设KM和KN的斜率分别为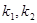 ,显然只需证
,显然只需证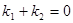 即可. ∵
即可. ∵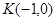 ,
,
∴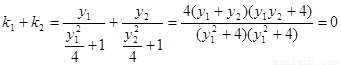 , 6分
, 6分
(2)设M、N的坐标分别为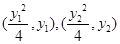 ,由M,O,P三点共线可求出P点的坐标为
,由M,O,P三点共线可求出P点的坐标为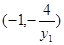 ,由N,O,Q三点共线可求出Q点坐标为
,由N,O,Q三点共线可求出Q点坐标为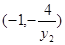 , 7分
, 7分
设直线MN的方程为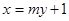 。由
。由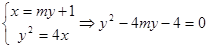
∴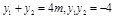 则
则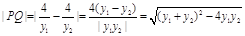
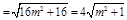 9分
9分
又直线MN的倾斜角为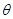 ,则
,则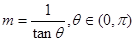
∴
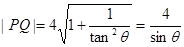 .10分
.10分
同理可得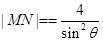 . 13分
. 13分
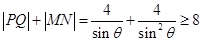 (
(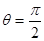 时取到等号) . 15分
时取到等号) . 15分
考点:1、抛物线的方程及性质;2、直线与曲线相交的性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

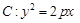 的焦点坐标为
的焦点坐标为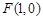 ,过
,过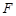 的直线交抛物线
的直线交抛物线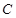 于
于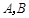 两点,直线
两点,直线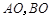 分别与直线
分别与直线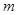 :
: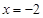 相交于
相交于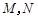 两点.
两点.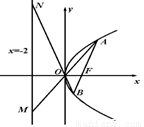
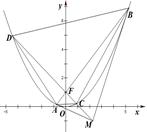
 的焦点为
的焦点为 ,过焦点
,过焦点 轴的动直线
轴的动直线 交抛物线于
交抛物线于 ,
, 两点,抛物线在
两点,抛物线在 .
.
 交该抛物线于
交该抛物线于 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值. 的焦点为
的焦点为 ,
, 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于 轴上方的点.
轴上方的点.  垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 (
( 为坐标原点).
为坐标原点).  的方程;
的方程; ,垂足为
,垂足为 ,求点
,求点 是
是 与圆
与圆