题目内容
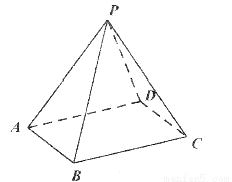
在底面是菱形的四棱锥 中,
中, .
.
(1)若 为线段
为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为线段
为线段 上的点,且
上的点,且 ,则
,则 为何值时,
为何值时, 平面
平面 ?
?
(3)若 分别为线段
分别为线段 的中点,求五面体
的中点,求五面体 的体积.
的体积.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
在底面是菱形的四棱锥 中,
中, .
.

(1)若 为线段
为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为线段
为线段 上的点,且
上的点,且 ,则
,则 为何值时,
为何值时, 平面
平面 ?
?
(3)若 分别为线段
分别为线段 的中点,求五面体
的中点,求五面体 的体积.
的体积.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案