题目内容
已知f(x)=
，则关于x的不等式f（3-x2）＜f（2x）的解集为（ ）
|
分析：作出函数f（x）的图象，根据图象可得函数的单调性，易知3-x2≤3，分情况讨论：当2x≤3时由单调性可去掉不等式中的符号“f”，得不等式组；当2x＞3时，若3-x2≥0，利用函数的对称性可化为函数的单调增区间内，同理用单调性可去掉符号“f”，得不等式组；当当2x＞3时，若3-x2＜0可把所给不等式表示出来，解不等式即可；
解答：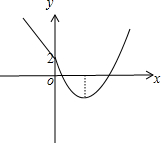
解：作出函数f（x）的图象，如右图所示：
显然3-x2≤3，
①当2x≤3时，由图象知f（x）在（-∞，3]上递减，在[3，+∞）上递增，
由f（3-x2）＜f（2x）得3-x2＞2x，
从而可得不等式组
，解得-3＜x＜1；
②当2x＞3时，若3-x2≥0，由y=x2-6x+2的图象关于x=3对称，得f（3-x2）=f（6-（3-x2））=f（3+x2），
则f（3-x2）＜f（2x）即f（3+x2）＜f（2x），由图象知f（x）在[3，+∞）上递增，有3+x2＜2x，
所以有不等式组
，此时无解；
③当2x＞3时，若3-x2＜0，由f（3-x2）＜f（2x），得2-（3-x2）＜（2x）2-6×2x+2，化简得x2-4x+1＞0，
从而可得不等式组
，解得x＞2+
；
综上可得f（3-x2）＜f（2x）的解集为：（-3，1）∪（2+
，+∞）．
故选D．
解：作出函数f（x）的图象，如右图所示：显然3-x2≤3，
①当2x≤3时，由图象知f（x）在（-∞，3]上递减，在[3，+∞）上递增，
由f（3-x2）＜f（2x）得3-x2＞2x，
从而可得不等式组
|
②当2x＞3时，若3-x2≥0，由y=x2-6x+2的图象关于x=3对称，得f（3-x2）=f（6-（3-x2））=f（3+x2），
则f（3-x2）＜f（2x）即f（3+x2）＜f（2x），由图象知f（x）在[3，+∞）上递增，有3+x2＜2x，
所以有不等式组
|
③当2x＞3时，若3-x2＜0，由f（3-x2）＜f（2x），得2-（3-x2）＜（2x）2-6×2x+2，化简得x2-4x+1＞0，
从而可得不等式组
|
| 3 |
综上可得f（3-x2）＜f（2x）的解集为：（-3，1）∪（2+
| 3 |
故选D．
点评：本题考查二次函数的单调性及其应用，考查不等式的求解，考查分类讨论思想、数形结合思想，考查学生分析解决问题的能力．
练习册系列答案
小学教材完全解读系列答案
相关题目
