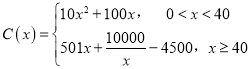题目内容
【题目】某学校为了研究期中考试前学生所做数学模拟试题的套数与考试成绩的关系，统计了五个班做的模拟试卷套数量及期中考试的平均分如下：
套（x） | 7 | 6 | 6 | 5 | 6 |
数学平均分（y） | 125 | 120 | 110 | 100 | 115 |
(Ⅰ) 若x与y成线性相关，则某班做了8套模拟试题，预计平均分为多少？
（2）期中考试对学生进行奖励，考入年级前200名，获一等奖学金500元；考入年级201—500 名，获二等奖学金300元；考入年级501名以后的学生生将不能获得奖学金。甲、乙两名学生获一等奖学金的概率均为
，获二等奖学金的概率均为
，.若甲、乙两名学生获得每个等级的奖学金是相互独立的，求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附： 
， 
。
【答案】（1）139. （2）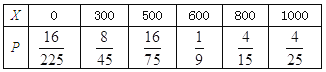 
E(X)=600
【解析】
（1）根据表格求出
，
，结合所给公式计算出
和
，得回归方程，将8代入即可得结果；（2）不获得奖学金的概率为
，X的取值可能为0，300，500，600，800，1000，计算出其概率得其分布列.
（1）.
，
，
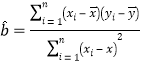
则
当
时，
即某班若做8套试题，预计平均分为139.
⑵不获得奖学金的概率均为
X的取值可能为0，300，500，600，800，1000
，
,
,
,
，，
即
的分布列为：
| 0 | 300 | 500 | 600 | 800 | 1000 |
|
|
|
|
|
|
|
练习册系列答案
阅读快车系列答案
相关题目
