题目内容
（2013•陕西）在一场娱乐晚会上，有5位民间歌手（1至5号）登台演唱，由现场数百名观众投票选出最受欢迎歌手．各位观众须彼此独立地在选票上选3名歌手，其中观众甲是1号歌手的歌迷，他必选1号，不选2号，另在3至5号中随机选2名．观众乙和丙对5位歌手的演唱没有偏爱，因此在1至5号中随机选3名歌手．
（Ⅰ） 求观众甲选中3号歌手且观众乙未选中3号歌手的概率；
（Ⅱ） X表示3号歌手得到观众甲、乙、丙的票数之和，求X的分布列和数学期望．
（Ⅰ） 求观众甲选中3号歌手且观众乙未选中3号歌手的概率；
（Ⅱ） X表示3号歌手得到观众甲、乙、丙的票数之和，求X的分布列和数学期望．
分析：（I）设事件A表示：“观众甲选中3号歌手且观众乙未选中3号歌手”，观众甲选中3号歌手的概率为
，观众乙未选中3号歌手的概率为1-
=
，利用互斥事件的概率公式，即可求得结论；
（II）由题意，X可取0，1，2，3，求出相应的概率，即可得到X的分布列与数学期望．
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
（II）由题意，X可取0，1，2，3，求出相应的概率，即可得到X的分布列与数学期望．
解答：解：（Ⅰ）设事件A表示：“观众甲选中3号歌手且观众乙未选中3号歌手”，
观众甲选中3号歌手的概率为
，观众乙未选中3号歌手的概率为1-
=
，
∴P（A）=
×(1-
)=
，
∴观众甲选中3号歌手且观众乙未选中3号歌手的概率为
；
（Ⅱ） X表示3号歌手得到观众甲、乙、丙的票数之和，则X可取0，1，2，3．
观众甲选中3号歌手的概率为
，观众乙选中3号歌手的概率为
，
当观众甲、乙、丙均未选中3号歌手时，这时X=0，P（X=0）=（1-
）（1-
）2=
，
当观众甲、乙、丙只有一人选中3号歌手时，这时X=1，
P（X=1）=
（1-
）2+（1-
）
（1-
）+（1-
）（1-
）
=
，
当观众甲、乙、丙只有二人选中3号歌手时，这时X=2，
P（X=2）=
•
（1-
）+（1-
）
•
+
（1-
）
=
，
当观众甲、乙、丙都选中3号歌手时，这时X=3，
P（X=3）=
•（
）2=
，
X的分布列如下：
∴数学期望EX=0×
+1×
+2×
+3×
=
．
观众甲选中3号歌手的概率为
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
∴P（A）=
| 2 |
| 3 |
| 3 |
| 5 |
| 4 |
| 15 |
∴观众甲选中3号歌手且观众乙未选中3号歌手的概率为
| 4 |
| 15 |
（Ⅱ） X表示3号歌手得到观众甲、乙、丙的票数之和，则X可取0，1，2，3．
观众甲选中3号歌手的概率为
| 2 |
| 3 |
| 3 |
| 5 |
当观众甲、乙、丙均未选中3号歌手时，这时X=0，P（X=0）=（1-
| 2 |
| 3 |
| 3 |
| 5 |
| 4 |
| 75 |
当观众甲、乙、丙只有一人选中3号歌手时，这时X=1，
P（X=1）=
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 20 |
| 75 |
当观众甲、乙、丙只有二人选中3号歌手时，这时X=2，
P（X=2）=
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 33 |
| 75 |
当观众甲、乙、丙都选中3号歌手时，这时X=3，
P（X=3）=
| 2 |
| 3 |
| 3 |
| 5 |
| 18 |
| 75 |
X的分布列如下：
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 4 |
| 75 |
| 20 |
| 75 |
| 33 |
| 75 |
| 18 |
| 75 |
| 28 |
| 15 |
点评：本题考查概率的计算，考查离散型随机变量的分布列与期望，解题的关键是确定变量的取值，求出相应的概率．
练习册系列答案
相关题目
（2013•陕西）如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF（该矩形区域内无其他信号来源，基站工作正常）．若在该矩形区域内随机地选一地点，则该地点无信号的概率是（ ）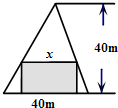
（2013•陕西）在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为
（2013•陕西）在如图所示的锐角三角形空地中，欲建一个面积不小于300m2的内接矩形花园（阴影部分），则其边长x（单位m）的取值范围是（ ）