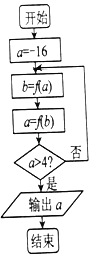
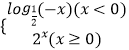题目内容
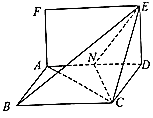
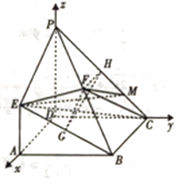
【题目】如图，已知四边形ABCD是正方形，EA⊥平面ABCD，PD∥EA，AD=PD=2EA=2，F，G，H分别为BP，BE，PC的中点． 
（1）求证：GH∥平面ADPE；
（2）M是线段PC上一点，且PM= 
，求二面角C﹣EF﹣M的余弦值．
【答案】
（1）证明：∵F，G，H分别为BP，BE，PC的中点，
∴GF∥PE，FH∥BC，
又四边形ABCD是正方形，∴BC∥AD，
∴FH∥AD，又PE与AD为相交直线，GF与FH为相交直线，
∴平面FGH∥平面ADPE，
∵GH平面FGH，
∴GH∥平面ADPE
（2）解：以D为原点，以DA，DC，DP为坐标轴建立空间直角坐标系如图：
则B（2，2，0），C（0，2，0），D（0，0，0），E（2，0，1），P（0，0，2），F（1，1，1），
∴ 
=（﹣1，1，0）， 
=（﹣2，2，﹣1）， 
=（﹣2，0，1）， 
=（0，2，﹣2），
∵PC=2 
，PM= 
，∴ 
= 
=（0， 
，﹣ ），
∴ 
= 
=（﹣2， ，﹣ 
），
设平面EFC的法向量为 
=（x1，y1，z1），平面EFM的法向量的 
=（x2，y2，z2），
则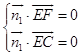 
， 
，
∴ 
， 
，
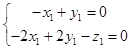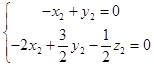令x1=x2=1得 =（1，1，0）， =（1，1，﹣1），
∴cos＜ ， ＞= 
= 
= 
．
∴二面角C﹣EF﹣M的余弦值为 ．
【解析】（1）利用中位线定理证明GF∥PE，FH∥BC，得出平面FGH∥平面ADPE，从而GH∥平面ADPE；（2）建立坐标系，求出平面EFC和平面EFM的法向量，计算法向量的夹角即可得出二面角的大小．
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
