题目内容
(本题14分)已知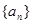 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,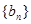 是等比数列,且
是等比数列,且 ,
,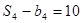 .
.
(Ⅰ)求数列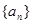 与
与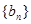 的通项公式;
的通项公式;
(Ⅱ)记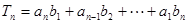 ,
,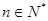 ,求
,求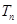 (
(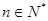 ).
).
【答案】
(1)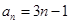 ,
,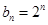 (2)
(2)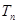
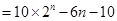
【解析】利用等差数列、等比数列的概念和性质及错位相减法求和等知识求解。
试题分析:(1)解:设等差数列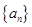 的公差为
的公差为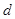 ,等比数列
,等比数列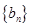 的公比为
的公比为 ,由题意,得
,由题意,得
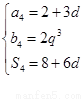 ,得到方程组
,得到方程组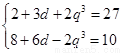 ,解得
,解得 ,
,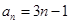 ,
,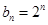
…………………………………………………………………………….7分
(2)证明: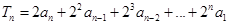 ,
,
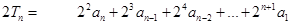 ,
,
相减,得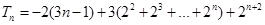
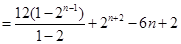
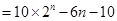
………………………………………………………………….14分
考点:本题主要考查了等差数列与等比数列的概念、通项公式、前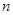 项和公式,数列求和等基础知识,考查化归与转化的思想方法,考查运算能力、推理论证能力。
项和公式,数列求和等基础知识,考查化归与转化的思想方法,考查运算能力、推理论证能力。
点评:解决此题的关键是掌握等差数列与等比数列的概念、通项公式、前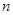 项和公式,错位相减求和等基础知识,本题难度不大。
项和公式,错位相减求和等基础知识,本题难度不大。

练习册系列答案
相关题目
 是递增数列,其前
是递增数列,其前 项和为
项和为 ,
, ,
, 且
且 ,
, .
. 的通项
的通项 ;
; ,使得
,使得 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的 的值;若不存在,请说明理由;
的值;若不存在,请说明理由; ,若对于任意的
,若对于任意的 ,不等式
,不等式 恒成立,求正整数
恒成立,求正整数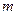 的最大值.
的最大值.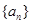 是递增的等差数列,
是递增的等差数列,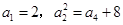 .
.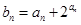 ,求数列
,求数列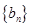 的前
的前 项和
项和 .
. (1)求
(1)求 (1)求
(1)求