题目内容
双曲线 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
(Ⅰ)求双曲线的离心率e;
(Ⅱ)若此双曲线过
 ,求双曲线的方程;
,求双曲线的方程;(Ⅲ)在(Ⅱ)的条件下,D1、D2分别是双曲线的虚轴端点(D2在y轴正半轴上),过D1的直线l交双曲线于点M、N,
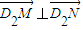 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(Ⅰ)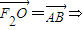 四边形F2ABO是平行四边形,由
四边形F2ABO是平行四边形,由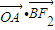 =0,知平行四边形F2ABO是菱形.由此能求出双曲线的离心率e.
=0,知平行四边形F2ABO是菱形.由此能求出双曲线的离心率e.
(Ⅱ)由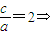 b2=c2-a2=3a2,双曲线方程为
b2=c2-a2=3a2,双曲线方程为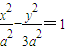 ,把点
,把点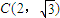 代入得a2=3,由此能求出双曲线方程.
代入得a2=3,由此能求出双曲线方程.
(Ⅲ)D1(0,-3),D2(0,3),设l的方程为y=kx-3,M(x1,y1),N(x2,y2),由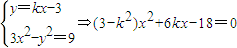 ,因l与与双曲线有两个交点,再由根的判别式和韦达定理进行求解.
,因l与与双曲线有两个交点,再由根的判别式和韦达定理进行求解.
解答: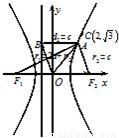 解:(Ⅰ)
解:(Ⅰ)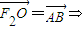 四边形F2ABO是平行四边形,
四边形F2ABO是平行四边形,
∴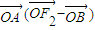 =0,即
=0,即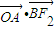 =0,
=0,
∴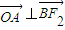 ,
,
∴平行四边形F2ABO是菱形.
如图,则r2=d1=c,r1=2a+r2=2a+c,
由双曲线定义得r1=d1e⇒2a+c=ce⇒e2-e-2=0,
∴e=2(e=-1舍去)(3分)
(Ⅱ)由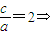 b2=c2-a2=3a2,
b2=c2-a2=3a2,
双曲线方程为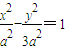 ,
,
把点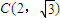 代入有得a2=3,
代入有得a2=3,
∴双曲线方程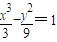 .(6分)
.(6分)
(Ⅲ)D1(0,-3),D2(0,3),
设l的方程为y=kx-3,M(x1,y1),N(x2,y2)
则由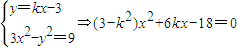 ,
,
因l与与双曲线有两个交点,∴3-k2≠0.
∵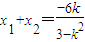 ,
, ,
,
△=36k2+4×18(3-k2)>0(8分)
∴ ,
,
y1•y2=k2x1x2-3k(x1+x2)+9=9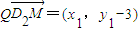 ,
,
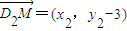 ,
,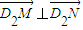 ⇒x1•x2+y1•y2-3(y1+y1)+9=0
⇒x1•x2+y1•y2-3(y1+y1)+9=0
∴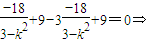 k2=5,
k2=5,
满足△>0,
∴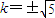 (11分)
(11分)
故所求直线l方程为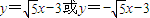 (13分)
(13分)
点评:本题考查双曲线的离心率和双曲线方程的求法,求直线方程.主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.
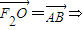 四边形F2ABO是平行四边形,由
四边形F2ABO是平行四边形,由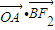 =0,知平行四边形F2ABO是菱形.由此能求出双曲线的离心率e.
=0,知平行四边形F2ABO是菱形.由此能求出双曲线的离心率e.(Ⅱ)由
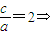 b2=c2-a2=3a2,双曲线方程为
b2=c2-a2=3a2,双曲线方程为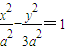 ,把点
,把点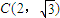 代入得a2=3,由此能求出双曲线方程.
代入得a2=3,由此能求出双曲线方程.(Ⅲ)D1(0,-3),D2(0,3),设l的方程为y=kx-3,M(x1,y1),N(x2,y2),由
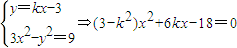 ,因l与与双曲线有两个交点,再由根的判别式和韦达定理进行求解.
,因l与与双曲线有两个交点,再由根的判别式和韦达定理进行求解.解答:
 解:(Ⅰ)
解:(Ⅰ)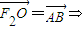 四边形F2ABO是平行四边形,
四边形F2ABO是平行四边形,∴
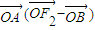 =0,即
=0,即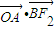 =0,
=0,∴
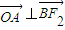 ,
,∴平行四边形F2ABO是菱形.
如图,则r2=d1=c,r1=2a+r2=2a+c,
由双曲线定义得r1=d1e⇒2a+c=ce⇒e2-e-2=0,
∴e=2(e=-1舍去)(3分)
(Ⅱ)由
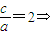 b2=c2-a2=3a2,
b2=c2-a2=3a2,双曲线方程为
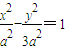 ,
,把点
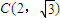 代入有得a2=3,
代入有得a2=3,∴双曲线方程
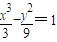 .(6分)
.(6分)(Ⅲ)D1(0,-3),D2(0,3),
设l的方程为y=kx-3,M(x1,y1),N(x2,y2)
则由
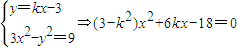 ,
,因l与与双曲线有两个交点,∴3-k2≠0.
∵
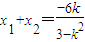 ,
, ,
,△=36k2+4×18(3-k2)>0(8分)
∴
 ,
,y1•y2=k2x1x2-3k(x1+x2)+9=9
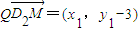 ,
,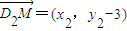 ,
,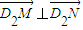 ⇒x1•x2+y1•y2-3(y1+y1)+9=0
⇒x1•x2+y1•y2-3(y1+y1)+9=0∴
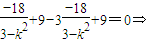 k2=5,
k2=5,满足△>0,
∴
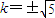 (11分)
(11分)故所求直线l方程为
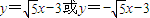 (13分)
(13分)点评:本题考查双曲线的离心率和双曲线方程的求法,求直线方程.主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆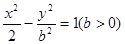 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· =
=