题目内容
12.过点(2,0)引直线l与曲线$y=\sqrt{2-{x^2}}$相交于A、B两点,O为坐标原点,当△AOB面积取得最大值时,直线l斜率为$-\frac{{\sqrt{3}}}{3}$.分析 由题意画出图形,求出使△AOB面积取得最大值时原点到直线l的距离,再由点到直线的距离公式求得直线l斜率.
解答 解:如图,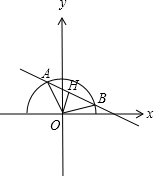
∵${S}_{△AOB}=\frac{1}{2}|OA||OB|sin∠AOB$=$\frac{1}{2}×\sqrt{2}×\sqrt{2}sin∠AOB≤1$,
当$∠AOB=\frac{π}{2}$时,S△AOB面积最大.
此时O到AB的距离d=1.
设AB方程为y=k(x-2)(k<0),
即kx-y-2k=0.
由$d=\frac{|2k|}{\sqrt{{k}^{2}+1}}=1$,解得k=-$\frac{\sqrt{3}}{3}$.
故答案为:$-\frac{\sqrt{3}}{3}$.
点评 本题考查了直线的斜率,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
4.已知A={x|x=3k-1,k∈Z},则下列表示正确的是( )
| A. | -1∉A | B. | -11∈A | C. | 3k+2∉A | D. | 3k2-1∈A |
 如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.
如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点. 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$(\sqrt{2},1)$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$(\sqrt{2},1)$. 已知函数f(x)=Msin(ωx+φ),(M>0,ω>0,$\frac{π}{2}≤φ≤π$)的部分图象如图所示,其中A,B两点之间的距离为5,那么f(-1)=2.
已知函数f(x)=Msin(ωx+φ),(M>0,ω>0,$\frac{π}{2}≤φ≤π$)的部分图象如图所示,其中A,B两点之间的距离为5,那么f(-1)=2.