题目内容
设关于![]() 的一元二次方程
的一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )有两根
)有两根![]() 和
和![]() 且满足
且满足![]() .①试用
.①试用![]() 表示
表示![]() ;②求证:数列
;②求证:数列![]() 是等比数列.
是等比数列.
③当![]() 时,求数列
时,求数列![]() 的通项公式.
的通项公式.
①![]() ②见解析③
②见解析③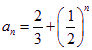
解析:
(1)根据韦达定理,得![]() ,
, ![]()
![]() ,由
,由![]()
得 ![]() ,故
,故![]()
(2)证明:![]() ,
,
若![]() ,则
,则![]() ,从而
,从而![]() ,
,
这时一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() 无实数根,故
无实数根,故![]() ,
,
所以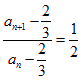 ,数列
,数列![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(3)设![]() ,则数列
,则数列![]() 是公比
是公比![]() 的等比数列,又
的等比数列,又
![]() ,所以
,所以 ,所以
,所以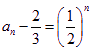 ,
,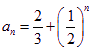 .
.

练习册系列答案
相关题目
题目内容
设关于![]() 的一元二次方程
的一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )有两根
)有两根![]() 和
和![]() 且满足
且满足![]() .①试用
.①试用![]() 表示
表示![]() ;②求证:数列
;②求证:数列![]() 是等比数列.
是等比数列.
③当![]() 时,求数列
时,求数列![]() 的通项公式.
的通项公式.
①![]() ②见解析③
②见解析③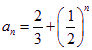
(1)根据韦达定理,得![]() ,
, ![]()
![]() ,由
,由![]()
得 ![]() ,故
,故![]()
(2)证明:![]() ,
,
若![]() ,则
,则![]() ,从而
,从而![]() ,
,
这时一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() 无实数根,故
无实数根,故![]() ,
,
所以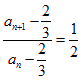 ,数列
,数列![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(3)设![]() ,则数列
,则数列![]() 是公比
是公比![]() 的等比数列,又
的等比数列,又
![]() ,所以
,所以 ,所以
,所以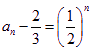 ,
,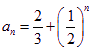 .
.
