题目内容
如图:正方体 的棱长为1,点
的棱长为1,点 分别是
分别是 和
和 的中点
的中点
(1)求证:
(2)求异面直线 与
与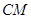 所成角的余弦值。
所成角的余弦值。
(1)连接 ,可得
,可得 。
。
由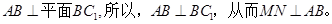
(2)
解析试题分析:(1)连接 ,因为, 点
,因为, 点 分别是
分别是 和
和 的中点,所以,
的中点,所以, 。
。
因为,正方体 中
中
(2)连接AC,因为, 所以,异面直线
所以,异面直线 与
与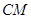 所成角即
所成角即 所成的角。连接AM,由正方体
所成的角。连接AM,由正方体 的棱长为1,点
的棱长为1,点 分别是
分别是 和
和 的中点,知,
的中点,知, ,所以,在三角形ACM中,由余弦定理得,异面直线
,所以,在三角形ACM中,由余弦定理得,异面直线 与
与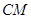 所成角的余弦值为,
所成角的余弦值为, 。
。
考点:异面直线的垂直,异面直线所成的角,余弦定理的应用。
点评:中档题,本题充分利用正方体中的平行关系、垂直关系,应用异面直线垂直的定义及异面直线所成角的定义,将空间问题转化成平面问题,利用勾股定理及余弦定理,使问题得到解决。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 、
、 为圆柱
为圆柱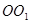 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 、
、 分别是
分别是 的中点,
的中点,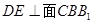 .
.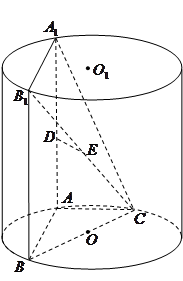
 ;
; ;
;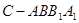 与圆柱
与圆柱 中,
中,
 底面
底面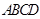 ,
, ,
, ,
, .
. 平面
平面 ;
;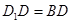 ,求四棱锥
,求四棱锥 的体积.
的体积.
 的4个顶点都在球
的4个顶点都在球 的表面上,
的表面上, 为球
为球 为球面上一点,且
为球面上一点,且 平面
平面  ,点
,点 为
为 的中点.
的中点.  平面
平面 ;
; 到平面
到平面 的距离.
的距离.
 的侧棱与底面
的侧棱与底面 垂直,底面
垂直,底面 ,侧棱
,侧棱 ,
, 分别是
分别是 与
与 的中点,点
的中点,点 在平面
在平面 上的射影是
上的射影是 的垂心
的垂心

 ;
; 的边长为2,
的边长为2, 分别为边
分别为边 的中点,
的中点, 是线段
是线段 的中点,如图,把正方形沿
的中点,如图,把正方形沿 .
.
 取何值,
取何值, 与
与 不可能垂直;
不可能垂直; 的大小为
的大小为 ,当
,当 时,求
时,求 的值.
的值. ,
, ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使 且
且 ,得一简单组合体
,得一简单组合体 如图2示,已知
如图2示,已知 分别为
分别为 的中点.
的中点.

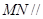 平面
平面 ;
; 
 ;
; 多长时,平面
多长时,平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ?
? 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.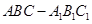 的所有棱长都为
的所有棱长都为 ,且
,且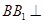 平面
平面 ,
, 为
为 中点.
中点.
 面
面 ;
; 的大小的余弦值;
的大小的余弦值; 到平面
到平面