题目内容
设A,B分别为椭圆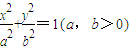 的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,证明点B在以MN为直径的圆内.
(此题不要求在答题卡上画图)
【答案】分析:(Ⅰ)根据题意可求得a和c的关系,进而根据准线方程求得a和c,则b可得,进而求得椭圆的方程.
(Ⅱ)根据(Ⅰ)中的椭圆方程可求得A,B的坐标,设出点M的坐标,代入椭圆方程,由P、A、M三点共线可以求得点P的坐标,进而表示出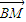 •
• 根据2-x>0判断出
根据2-x>0判断出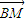 •
•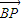 >0,进而可知∠MBP为锐角,从而∠MBN为钝角,判断出点B在以MN为直径的圆内.
>0,进而可知∠MBP为锐角,从而∠MBN为钝角,判断出点B在以MN为直径的圆内.
解答: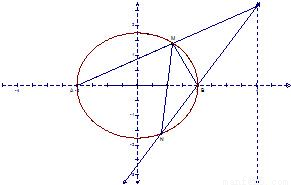 解:(Ⅰ)依题意得a=2c,
解:(Ⅰ)依题意得a=2c,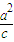 =4,
=4,
解得a=2,c=1,从而b=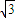 .
.
故椭圆的方程为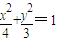 .
.
(Ⅱ)由(Ⅰ)得A(-2,0),B(2,0).
设M(x,y).
∵M点在椭圆上,
∴y2= (4-x2)(1)
(4-x2)(1)
又点M异于顶点A、B,
∴-2<x<2,由P、A、M三点共线可以得
P(4,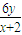 ).
).
从而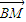 =(x-2,y),
=(x-2,y),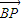 =(2,
=(2,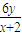 ).
).
∴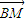 •
•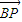 =2x-4+
=2x-4+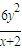 =
= (x2-4+3y2).(2)
(x2-4+3y2).(2)
将(1)代入(2),化简得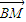 •
•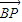 =
= (2-x).
(2-x).
∵2-x>0,
∴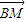 •
•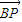 >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.
(Ⅱ)根据(Ⅰ)中的椭圆方程可求得A,B的坐标,设出点M的坐标,代入椭圆方程,由P、A、M三点共线可以求得点P的坐标,进而表示出
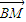 •
• 根据2-x>0判断出
根据2-x>0判断出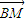 •
•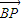 >0,进而可知∠MBP为锐角,从而∠MBN为钝角,判断出点B在以MN为直径的圆内.
>0,进而可知∠MBP为锐角,从而∠MBN为钝角,判断出点B在以MN为直径的圆内.解答:
 解:(Ⅰ)依题意得a=2c,
解:(Ⅰ)依题意得a=2c,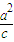 =4,
=4,解得a=2,c=1,从而b=
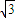 .
.故椭圆的方程为
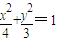 .
.(Ⅱ)由(Ⅰ)得A(-2,0),B(2,0).
设M(x,y).
∵M点在椭圆上,
∴y2=
 (4-x2)(1)
(4-x2)(1)又点M异于顶点A、B,
∴-2<x<2,由P、A、M三点共线可以得
P(4,
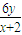 ).
).从而
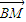 =(x-2,y),
=(x-2,y),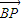 =(2,
=(2,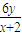 ).
).∴
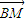 •
•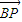 =2x-4+
=2x-4+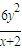 =
= (x2-4+3y2).(2)
(x2-4+3y2).(2)将(1)代入(2),化简得
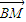 •
•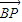 =
= (2-x).
(2-x).∵2-x>0,
∴
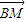 •
•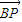 >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,故点B在以MN为直径的圆内.
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
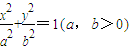 的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.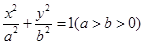 的左、右顶点,椭圆的长轴长为4,且点
的左、右顶点,椭圆的长轴长为4,且点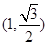 在该椭圆上。
在该椭圆上。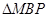 为锐角三角形
为锐角三角形