题目内容
19.函数y=f(x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,$\frac{π}{n}$]上的面积为$\frac{2}{n}$(n∈N*),则函数y=sin(3x-π)+1在[$\frac{π}{3}$,$\frac{4π}{3}$]上的面积为( )| A. | π+$\frac{8}{3}$ | B. | π+2 | C. | π+1 | D. | π+$\frac{2}{3}$ |
分析 通过数形结合,画出图象即可.
解答 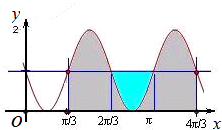 解:y=sin(3x-π)+1=-sin3x+1,
解:y=sin(3x-π)+1=-sin3x+1,
其图象是由y=-sin3x的图象向上平移一个单位得到的,
将所求的面积涂上阴影(如图),可以看出,
将y=1以上的一个凸形切下来,补到凹形上,
阴影部分正好是一个长为π、宽1的矩形,即面积为π,
∵函数y=sinnx在[0,$\frac{π}{n}$]上的面积为$\frac{2}{n}$(n∈N*),
∴y=1以上的一个凸形的面积为$\frac{2}{3}$,
∴所求面积为π+$\frac{2}{3}$,
故选:D.
点评 本题考查面积的计算,考查数形结合,利用割补法是解决本题的关键,属于中档题.

练习册系列答案
相关题目
4.已知直线l1:mx+8y+n=0和l2:2x+my-1=0.则“m=4且n≠-2”是“l1∥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.